Návod na Confetti sudoku ze 406. kola dlouhodobé soutěže

Představuji kratší návod na úlohu Confetti sudoku ze 406. kola dlouhodobé soutěže (DS). Tvorbu úlohy inspirovalo vědomí, že se stejný typ měl vyskytnout v kvalifikaci pro Německé sudokové mistrovství 2021, která proběhla minulý lednový víkend. Osobně jsem prvně Confetti sudoku spatřil v Riadově Sudoku September Contestu 2018 na LMI.

Z výsledků DS 406. kola jsem si všiml, že dost luštitelů, kteří vyluštili tabulku malou, už nezvládli tu větší. Co vám asi uniklo?  Pokusím se přiblížit řešení následujícím návodem.V něm bych chtěl taktéž představit 2 principy, které mohou při luštění úlohy pomoci.

Prvním principem je jak se chovat, když máme něco v úloze odhalit. Informace může být v úloze zakódovaná, skrytá (což se týká našeho Confetti sudoku) nebo ji dostaneme jen dílčí, což bývá např.u sudoku s okrajovou nápovědou. Jako pomoc k řešení je dobré si uvědomit, jaké jsou všechny možnosti, dopočítat je, vypsat si je, sledovat je během luštění, prostě si v tom udělat pořádek a systém.  Někdy ani to nestačí a je nutné kombinovat možné varianty, které nám zbývají.

Druhou věcí je, že úlohy typu sousledné sudoku, kropki a podobné nám udávají v tabulce vztahy vzhledem k paritě čísel. U sousledného sudoku nemusím paritu vůbec využít, ale když je někde čárka souslednosti vím, že jedno číslo je sudé a druhé liché. Informace o paritě pro konkrétní buňku, potažmo o vztazích mezi sudými a lichými čísly v řádku, sloupci či čtverci 3x3 nám, nám pomáhá odhalit hledaná čísla.

Pojďme na Confetti sudoku, zadání úlohy z DS bylo následující:

Doplň do všech prázdných polí tabulky čísla 1–6 (1-9) tak, aby se čísla neopakovala v žádném řádku, sloupci ani tučně ohraničeném regionu 2×3 (3x3). 

V tabulce jsou vyznačeny kolečky všechny dvojice čísel, jejichž rozdíl činí 3 různé hodnoty, nazvěme je A, B a C. Všechny dvojice čísel s rozdílem hodnot A mají mezi sebou bílé kolečko, všechny dvojice čísel s rozdílem hodnot B mají mezi sebou šedé kolečko, všechny dvojice čísel s rozdílem hodnot C mají mezi sebou černé kolečko. Odhalit, jaké čísla představují hodnotu rozdílu A, B a C, je součástí řešení úkolu.

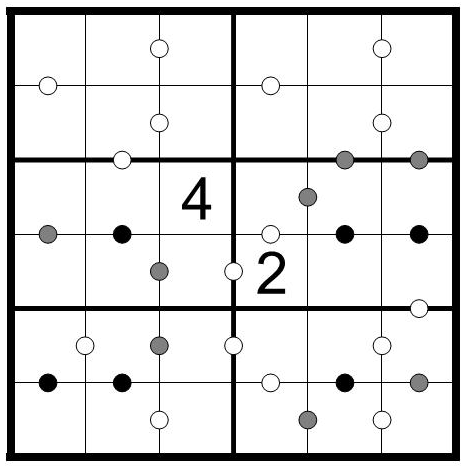
V tabulce jsou vyznačena kolečka, které představují rozdíl sousedních čísel. Zároveň jsou všechna kolečka vyznačena, nezapomínat tedy na použití záporné podmínky, kdykoli je to možné. Já si u tabulek vypíšu všechny rozdíly, které kolečka mohou představovat, a budu s nimi pracovat během luštění.

V sudoku 6x6 může být rozdíl mezi sousedními čísly pouze 1, 2, 3, 4 nebo 5. Kolečka všech tří barev se vyskytují vícekrát v alespoň jednom řádku, sloupci nebo čtverci 3x3, mohu tedy vyloučit rozdíl 5, který mohou představovat pouze čísla 1 a 6. Bílé kolečko se vyskytuje v 1. a 2. čtverci třikrát, mohu tedy vyloučit rozdíl 4, jelikož ho lze z čísel 1-6 vytvořit pouze dvakrát (1-5 a 2-6). Dále mohu vyloučit pro bílé kolečko rozdíl 2, protože u zadané dvojky (4. řádek, 4. sloupec) bych nemohl najít jiného kamaráda než číslo 4, což nelze. Jinak lze nepoužitelnost rozdílu 2 vydedukovat z přítomnosti 3 koleček v jednom čtverci 3x3, kde mohu stvořit pouze dvojici 4 s číslem 2 nebo 6 a dvojici čísla 3 s číslem 1 nebo 5. Ale třetí dvojice je bez šance. Šedé kolečko nám na první pohled nic neříká, to černé kolečko ano. Pokud by rozdíl u černého kolečka odpovídal číslu 3, tak z šestice čísel 1-6 vytvořím vždy tři trojice, a to 1-4, 2-5, 3-6. Tím pádem v místech, kde se již dvě takové dvojice vyskytují (viz 4. čtverec, 5. čtverec nebo 5. sloupec), by při uvědomění si záporné podmínky muselo být u zbylé dvojice polí třetí černé kolečko, ale ono tam není. Podobný postup mohu uplatnit u černého kolečka pro rozdíl 1 ve čtvrtém čtverci. Ve dvojicích nemohu využít číslo 2, které je zapsáno mimo černá kolečka. Dvojice by tedy tvořila čísla 3-4 a 5-6, zbývající a navzájem sousedící políčka by zabírala čísla 1 a 2. Čímž by se čísla lišila o 1 a muselo by tam být černé kolečko. Je tam kolečko bílé a to podle pravidel úlohy, kdy všechny 3 rozdíly jsou představovány jiným kolečkem, nelze. Černé kolečko tedy představuje rozdíl 2. 

S tímto vědomím mohu hned doplnit číslo 4 (4. řádek, 6. sloupec) při využití negativní podmínky s číslem 2, s kterým by mohlo sousedit jedině v případě přítomnosti černého kolečka. Do dvojičky s číslem 4 doplním číslo 6. Další a možná pro někoho zábavnou, pro jiného zas nimravou prací, vyplníme zbytek tabulky a dopátráme se i k odhalení hodnoty ostatních koleček.

Pokud je v tabulce doplněno dostatečné množství koleček, určitě by se našla místa, z kterých lze vypátrat informace, které by se hodily k řešení úlohy. Příkladem budiž první sloupec, kde se nachází tři dvojice se třemi různými kolečky. Schválně si zkuste za domácí úkol napsat všechny možnosti vyplnění prvního sloupce.  Mně vzájemnou kombinací čísel vychází, že trojice rozdílů bude buď 1-2-4, 2-3-4 nebo 1-3-5, přitom poslední sekvenci jsme již kvůli rozdílu 5, který nejde uplatnit, vyloučili. U sudoku 6x6 je toto asi zbytečné, ale u jiných těžších logických nemravností může taková informace být jediným schůdným krokem k řešení.

Přesuňme se k větší tabulce. Opět si k tabulce vypíšu rozdíly 1-8, abych s nimi během luštění mohl pracovat. První úvahy jsou obdobné jako u tabulky malé, mohu aplikovat největší rozdíl 8? Všechny tři barvy koleček se vyskytují vícekrát alespoň v jednom řádku, sloupci nebo čtverci 3x3, nemůže tedy rozdíl 8 být přiřazen ani jednomu kolečku. Ba co víc. Bílé a černé kolečko tabulku celkem zavšivilo, ale i šedé kolečko se v třetím sloupci vyskytuje 2x, plus jedno další pole je spojeno s šedým kolečkem. Nemohu tedy pro žádné kolečko uplatnit rozdíl 7, kterému náležejí pouze dvojice čísel 1-8 nebo 2-9.

Při kontrole tabulky na mě doslova vybafnul 4. čtverec, vidíte to?  Ve 4. čtverci se nachází dvě sekvence polí s bílými kolečky, jedna dlouhá pět polí, druhá tři pole. Bílé kolečko je tedy představováno rozdílem 1 nebo rozdílem 2. V druhém případě by delší sekvence zabírala lichá čísla 1-3-5-7-9, kratší čísla sudá. K mé radosti mohu rozseknout tuto úvahu hned v zápětí, jelikož si všimnu, že zadaná 4 na prvním řádku je spojena bílým kolečkem a v případě rozdílu 1 by kamarád do páru bylo pouze číslo 3 nebo 5, které však už jsou v prvním řádku zadané. Bílé kolečko tudíž představuje rozdíl 2.

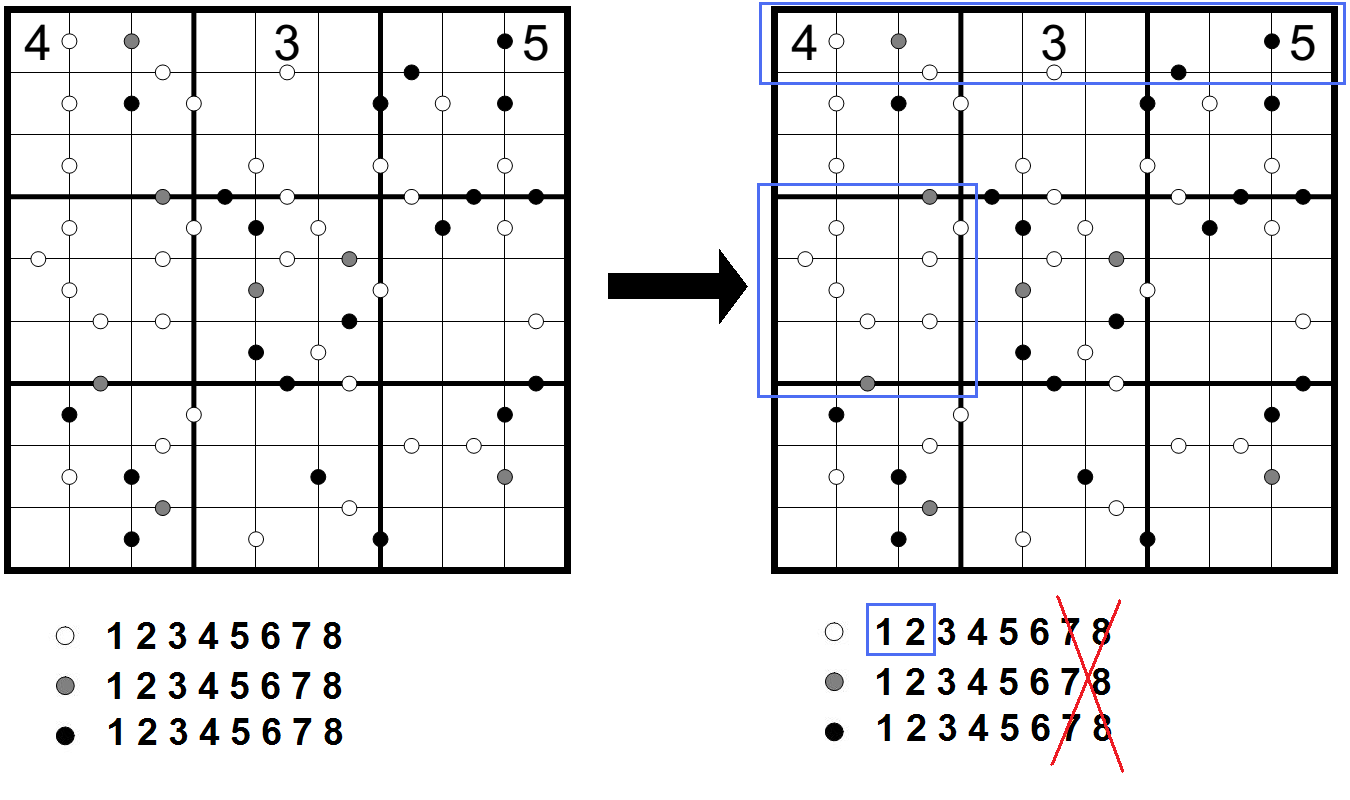
Filozofování bylo dost, nastal čas se do luštění pořádně opřít. Bílé kolečko se vyskytuje v tabulce nejčastěji a já nyní vím, že každá dvojice čísel spojena bílým kolečkem bude mít stejnou paritu. Dále vím, že v každém řádku, sloupci či čtverci 3x3, kde se nacházejí 4 oddělené dvojice bílých koleček, bude deváté políčko liché, protože z čísel 1-9 mohu vytvořit dvě sudé dvojice 2-4 a 6-8 a dvě liché dvojice. To se týká 3. a 4. řádku. Dále pokud se někde nachází již tři sudá pole, vím, že další dvojička spojená bílým kolečkem bude lichá. Podobnými úvahami se dá v této chvíli doslova vyřádit. Během zabarvování si všimnu, že se mi obarvila dvojice polí spojených šedých kolečkem políčky opačné parity, černé kolečko spojují políčka stejné parity. Rozdíl představující šedé kolečko může tedy být pouze 1, 3 nebo 5, černé kolečko představuje rozdíl 4 nebo 6. Paritní hrátky mi pomůžou dobarvit celou tabulku do podoby jakéhosi sudolichého sudoku.

Nyní lze snadněji doplňovat čísla či alespoň vpisky. V prvním čtverci mám dvě sudé dvojičky s bílým kolečkem, tvoří je 2-4 a 6-8. Do 4. čtverce si mohu napsat vztahy zmíněné v textu dříve, pětipolíčková sekvence bude mít uprostřed 5, sudý sirotek v témže čtverci bude obsahovat jedno z krajních sudých čísel 2 nebo 8.

Co vymyslet dále? Číslo 5 s černým kolečkem nemůže mít kamaráda o 6 většího či menšího, černé kolečko bude představovat rozdíl 4. Nyní bych se pokusil o úvahu v 3. čtverci, kde jsou tři černá kolečka. Všechny možné dvojice s rozdílem 4 jsou 1-5, 2-6, 3-7, 4-8 a 5-9. Číslo 5 se vyskytuje ve dvou dvojicích. Pokud je 5 jako v našem případě už přítomno v jedné dvojici, pak nepoužité číslo 1 nebo 9 bude sirotek na jiném lichém poli bez černého kolečka. Ve 3. čtverci jsou daší dvě černokolečkové dvojice sudé, tedy 2-6 a 4-8, a výsledkem je, že mi zbývá dvojička čísel 3 a 7. Jelikož je nemohu ve 3. řádku napsat vedle sebe, poněvadž by muselo být vyznačeno čtvrté černé kolečko, mohu si do 3. řádku 8. sloupce napsat vpisku 19 a obklopit ji vpiskama 37 na třetím řádku. Udělal jsem krok jakési nesouslednosti o 4, jinak řečeno jsem využil negativní podmínky, že všechna možná kolečka jsou v tabulce vyznačena. A zapsané 19 mi vykouzlí hned číslo 5 na 4. řádku v 8.sloupci.

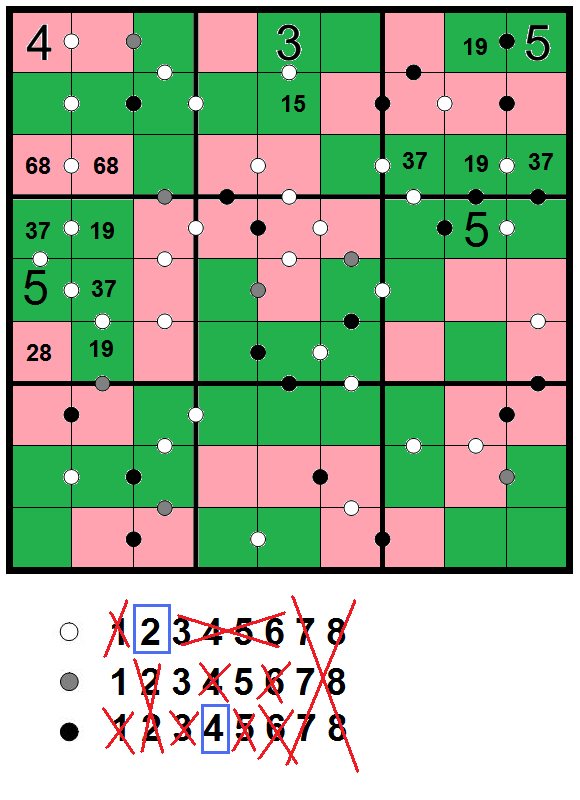
Myslím, že mých úvah už bylo dost, se zbytkem si poradíte.  Pokud byste nebyli Confeťákem nabaženi, zkuste Riadovu verzi nebo úlohu z německé kvalifikace, ta byla zas úplně o něčem jiném, koleček tam bylo pomálu ...

sepsal Pavel Kadlečík

Další návody na řešení úloh:
Renban sudoku z MČRS 2020
Hanidoku
Antidiagonální zabijáček
Tipy na úlohy z českého kola Sudoku GP 2020
Zabijáček
Sudoku klony