Následuje návod na úlohu Zabijáček alias Little Killer s částečnou legendou kolem tabulky. Autorem úlohy je Bernhard Seckinger a byla použita na Mistrovství Německa v sudoku 2019. Návod byl sepsán v rámci přípravy na MS 2019 v Německu.
Pro pravidla úlohy zabijáček platí, že každý řádek, sloupec a zvýrazněný region obsahuje čísla 1-9, každé právě jednou. Po okraji tabulky jsou vyznačena čísla se šipkami, každé číslo udává součet všech čísel na diagonále, na níž ukazuje šipka. Čísla se na diagonále mohou opakovat.
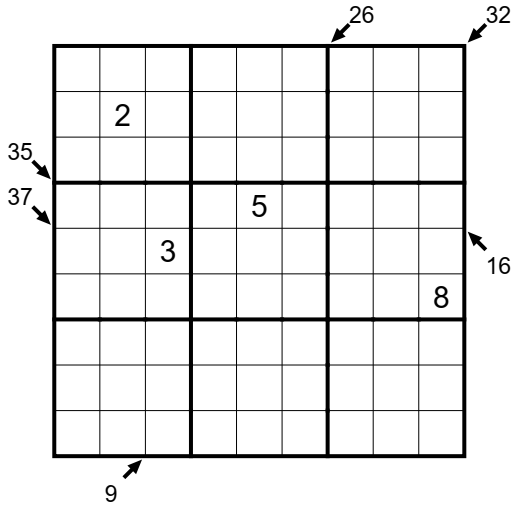
Postup řešení se u zabijáčka s částečnou legendou může lišit od postupu k zabijáčku s uvedenými součty na všech diagonálách, kdy si všímám zpravidla nejdříve součtů pro diagonály o 1 poli, 2 polích, 3 polích. U částečné legendy s 6 zadanými součty předpokládám, že autor vyznačil právě tolik diagonál, kolik je potřeba k vyřešení sudoku. Tudíž vím, že musím během luštění rozlousknout čísla na všech vyznačených diagonálách, abych se dopracoval k řešení.
Jako pomůcku jsem si barevně zvýraznil všech 6 diagonál, jednak abych se soustředil právě na ně, a pak abych dále odhalil místa, kde se diagonály kříží a platí pro ně vztah s diagonálou další. Při řešení budu tedy využívat (a) součet čísel na diagonálách, (b) polí, kde se kříží vyznačené diagonály, (c) všechny další čísla, která se mi vyloupnou z technik klasického sudoku a která v zadáních s málo čísly a málo nápovědami bychom měli neustále při řešení využívat jako ochranu proti nešvaru jménem čuming. :-) Pracovně jsem si ještě pojmenoval diagonálu, kde se snažím součet maximalizovat, tj. doplnit co největší čísla, abych dosáhl součtu, jako diagonálu vysokou a diagonálu, kterou se snažím minimalizovat co nejmenšími čísly, abych se do součtu vešel, jako diagonálu nízkou.
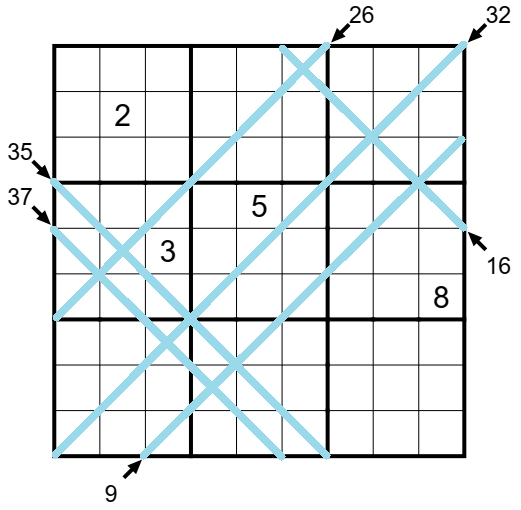
Pojďme na to. Zprvu hledám nízké a vysoké diagonály, kde mě to opravdu trkne, že tam buď čísla doplním nebo napíšu dvojičky (trojičky) vpisků na místa, která jasná nebudou. Psát si možnosti součtů zprvu hned pro všechny diagonály je zbytečné a zabírá čas. Jako první vidím vysokou diagonálu na 5 polí se součtem 37 a nízkou diagonálu na 7 polí se součtem 9. Diagonála se součtem 37 mi ale nabízí spoustu možností a vyřazení jen několika čísel, teď se s ní zabývat nebudu! Ale diagonála 9 na 7 polí mohu rovnou doplnit. A hle, ona ta 37čka zas není tak od věci, na křížení dvou zmíněných diagonál se mi objevil dvojpisek čísel 1 a 2.
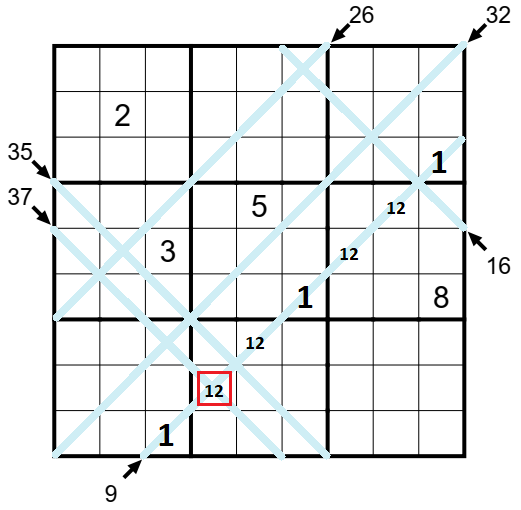
Na vysokou 37čku se snažím nacpat co nejvyšší čísla, aby dosáhl součtu 37 a s případnou 1 na křížení diagonál neuspěji. Bude tam tedy číslo 2. Mohu si na diagonálu doplnit všechna čísla (8 a 9) a hned si všímám pole, kde se vysoká diagonála 37 kříží s teď již bezesporu nízkou diagonálou 32 o 9 polích, kam jsem do jednoho pole umístil číslo 9.
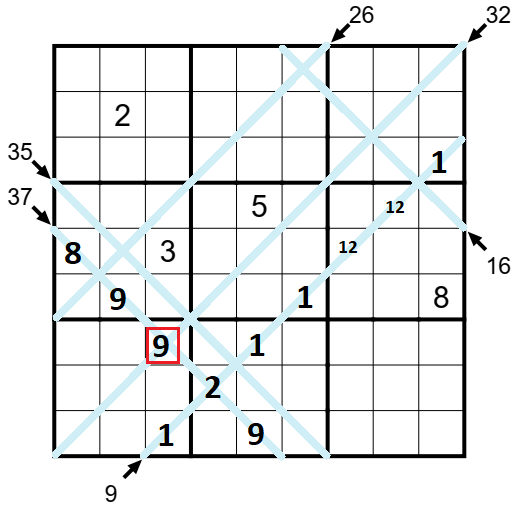
Nízká diagonála 32 prochází třemi čtverci 3x3, v nichž je již zapsáno číslo 1. Nejmenší možný součet, který tak lze ve čtvercích 3x3 na diagonále 32 dosáhnout, je tedy součet 9 (z čísel 234) v 3.čtverci, stejný součet v 5.čtverci a s již zapsaným číslem 9 v 7.čtverci je to součet 15 (9 + čísla 2 a 3). Což nám celkem dává oněch požadovaných 32, zapišme čísla do tabulky.
Dvakrát jsme tedy využili kroku, kdy se křížila nízká diagonála s vysokou, teď se nám nabízí situace, kdy se dvě nízké diagonály ve 3. čtverci sice nekříží, ale obě diagonály (tj. 32ka s 16tkou) se nacházejí v jednom čtverci 3x3 a já potřebuji na diagonálu 16 také zapsat nízká čísla.
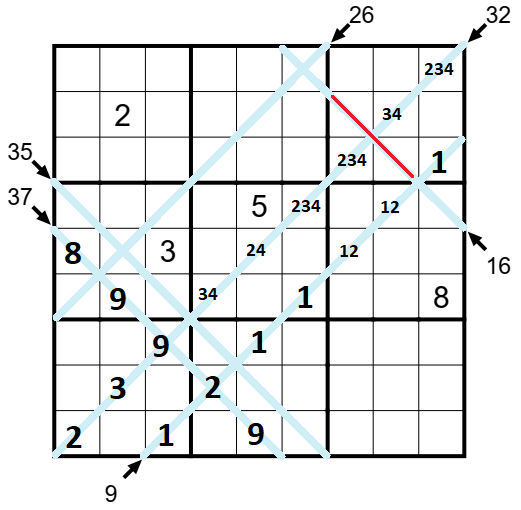
Dvě pole na diagonále 16 a zároveň ve 3. čtverci 3x3 mohou obsahovat součet 11 (tj. minimální s čísly 5 a 6) až součet 14. Na dvě pole 16tky mimo 3.čtverec již ale nejde zapsat číslo 1, na pole 16tky v 6. čtverci nejde ani číslo 2, z čehož zbývá jediná možnost vyplnění diagonály 16 shora dolů 2 - vpisky 56 - vpisky 56 - 3. V tuto chvíli se již nabízí hrát techniky klasického sudoku, v tabulce jsme zadali např. již dost čísel 1, 2 a 3. A dostaneme se tak do situace, kdy na vysokou diagonálu 35 zapíšeme číslo 2 (6.řádek, 3.slupec).
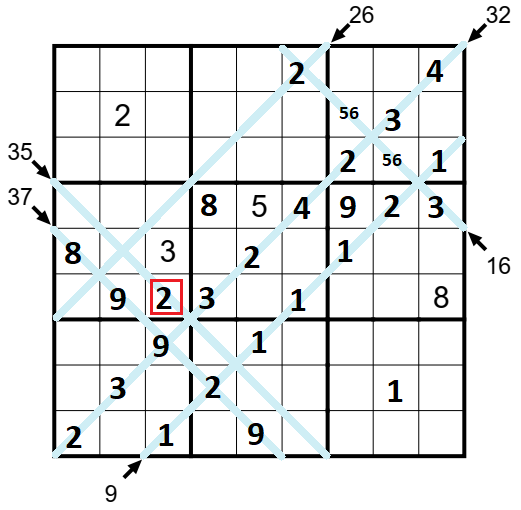
Na vysoké diagonále se snažíme dávat vysoká čísla, abychom ji složili. Ve 4.čverci 3x3 se na jedno pole 35tky cpe číslo 4, kdybychom si ale dopočítali zbytek diagonály při zadání nejvyšších možných čísel, nedopočítáme se s použitím čísla 4 do součtu 37 (max. jen 36), musí tak na toto pole (5.řádek, 2. sloupec) přijít číslo 5 a na zbývající prázdná pole diagonály 35 doplníme nejvyšší možná čísla. Opět tabulku zaplníme čísly z klasického sudoku a už nám zbývá dokončit jen diagonálu 26.
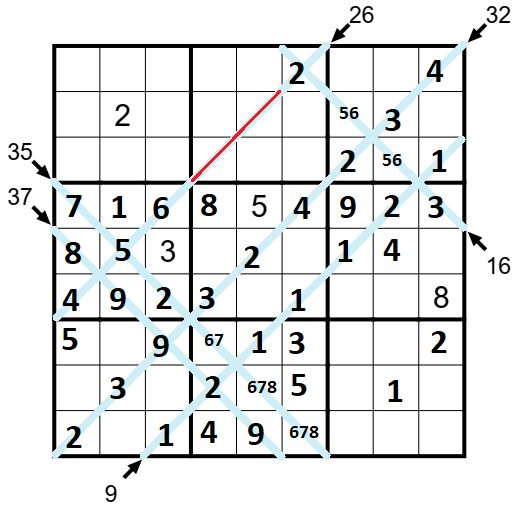
Diagonálu 26 nebudu nazývat nízkou ani vysokou, na zbývající dvě pole potřebuji jednoduše zadat čísla se součtem 9 a ze současné situace lze zapsat pouze čísla 4 a 5. V tuto chvíli jsem již zadal všechna čísla na diagonály, k dořešení zabijáčka tak budu potřebovat pouze techniky klasického sudoku.
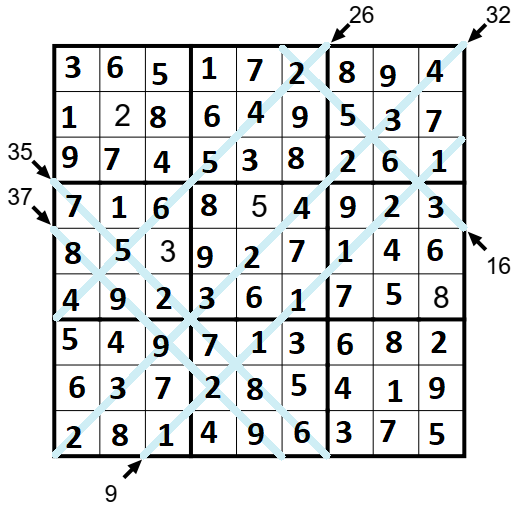
Pokud by měla stejná úloha kompletní legendu (= uvedeny součty všech možných diagonál), nemuselo by být vůbec lehké najít právě zmíněných 6 diagonál, které stačí k vyřešení úlohy. Pravděpodobně bychom řešili úlohu jinak. Jako pomůcku uvádím maximální součty všech diagonál (od jednopolíčkové po devítipolíčkovou) 9 - 17 - 24 - 35 - 43 - 48 - 61 - 69 - 72 a minimální součty všech diagonál 1 - 3 - 6 - 5 - 7 - 12 - 9 - 11 - 18.
Koho úloha bavila, podobné zabijáčky vytvořil Fred Stalder nebo Bastien Vial-Jaime. V Dlouhodobé soutěži se zabijáček objevil v 68. kole nebo ve 330. kole.
sepsal Pavel Kadlečík
Theme by Danetsoft and Danang Probo Sayekti inspired by Maksimer