Následuje návod na na úlohu Antidiagonální zabijáček 9x9, která byla zařazena do 374. kola dlouhodobé soutěže. Úlohu jsem stvořil na památku Marušky Benediktové (alias Cauchy) s vědomím, že ona sama tvořila zabijáčky a antidiagonální sudoku, i když jsem takovou úlohu nikdy dříve neviděl.
Před časem jsem publikoval návod na zabijáčka, pokud byste se chtěli více vnořit do podstaty jeho luštění, zkuste si ho též přečíst. Zde se budu snažit více věnovat antidiagonálnímu sudoku, i když k vyluštění úlohy a k s pocitu radosti při luštění budeme potřebovat kroky vyplývající z technik luštění obou variant.
Pro pravidla úlohy zabijáček platí, že každý řádek, sloupec a zvýrazněný region obsahuje čísla 1-9, každé právě jednou. Po okraji tabulky jsou vyznačena čísla se šipkami, každé číslo udává součet všech čísel na diagonále, na níž ukazuje šipka. Čísla se na diagonále mohou opakovat. Pro pravidla antidiagonálního sudoku 9x9 platí, že na obou diagonálách se vyskytují vždy 3 stejná čísla.
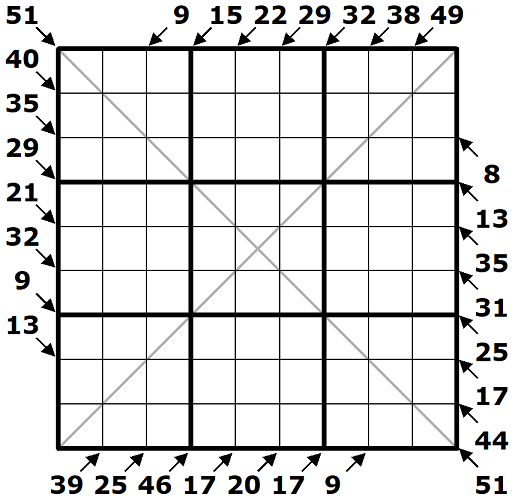
V antidiagonálním sudoku se doporučuji prvně zaměřit na odhalení trojice čísel ležící na diagonálách. Fakt, že leží na diagonále a ostatní čísla tam ležet nemohou, lze využít při luštění technikami klasického sudoku. Pokud bychom úspěšní hned nebyli a určili například skupinu 5 čísel, z kterých budeme vybírat příslušnou trojici, i tak to může být cenná informace (příkladem můžeme zjistit, že dvě čísla z této skupiny nemohou zároveň ležet na diagonále, protože do vybraného čtverce jdou zapsat jen na totéž místo diagonály apod.) Velmi důležitým místem antidiagonálního sudoku je středový 5. čtverec, kde se střetávají obě diagonály. Středové pole tabulky bude okupovat číslo náležící do obou diagonálních trojic, zbylé dva páry tvoří čísla různá. Konec přednášky, jdeme luštit!
Pro přehlednost textu budu diagonálu vedoucí z levého horního rohu do pravého dolního rohu nazývat diagonálou klesající, diagonálu vedoucí z levého dolního rohu vzhůru do pravého horního rohu diagonálou roustoucí. K principům antidiagonálního sudoku se budeme v průběhu luštění vracet, luštění začněme zabijáčkem. Pokud je kolem zabijáčka zadáno mnoho čísel či rovnou všechna, nejlépe se věnovat těm, které zaujmou vaší pozornost. Součty 1-, 2- a 3-políčkových diagonál využijeme takřka vždycky, pokud jsou zadány.
V horní řadě mě nezaujalo vůbec žádné zadané číslo, v pravém sloupci číslo 35 na 4 pole, dále 17 na 7 polí a samozřejmě číslo 51, které udává třikrát součet trojice čísel klesající diagonály. Budu se tudíž při dalším luštění upínat k součtu 17 pro hledanou trojici. Na spodním řádku je výrazné číslo 46 na 6 polí a v levém sloupci číslo 32 na 4 pole. Pokud bych si chtěl ověřit, zda můj odhad byl správný, zkusím zadané součty porovnat s maximálními a minimálními součty, které se na diagonálách mohou vyskytovat. Toto uvádím jen pro zajímavost, při soutěžním luštění na podobné analýzy nebývá čas. ![]()
| MIN | 1 | 3 | 6 | 5 | 7 | 12 | 9 | 11 | 18 |
| MAX | 9 | 17 | 24 | 35 | 43 | 48 | 61 | 69 | 72 |
| horní řada | 9 | 15 | 22 | 29 | 32 | 38 | 49 | ||
| pravý sloupec | 8 | 13 | 35 | 31 | 25 | 17 | 44 | 51 | |
| dolní řada | 9 | 17 | 20 | 17 | 46 | 25 | 39 | ||
| levý sloupec | 13 | 9 | 32 | 21 | 29 | 35 | 40 | 51 |
Součet 35 mohu rovnou zapsat pomocí třech 9 a jedné 8, na číslo 48 budu myslet, že ho tvoří součty 23 a 23 nebo 22 a 24. Ostatní součty jsou příliš vzdáleny od maximálních či minimálních možných a nabízejí tak příliš mnoho kombinací. Uvažovat by šlo o zmíněném součtu 32 v levém sloupci, ale vyžaduje to zapsání čtyřvpisků a pětivpisků, což může být spíše matoucí.
Čeho si je ale nutno všimnout je, že u všech diagonál vedoucí zleva vpravo dolů je uveden součet až na dvě 1-políčkové diagonály zaplňující rohy. Pokud totiž sečtu všechny takové diagonály, dopátrám se čísla 403. Součet všech čísel tabulky činí 9 * 45 = 405, tudíž jen o dvě více. Právě jsem odhalil největší fintu celé úlohy, do levého dolního a pravého horního rohu doplním čísla 1.
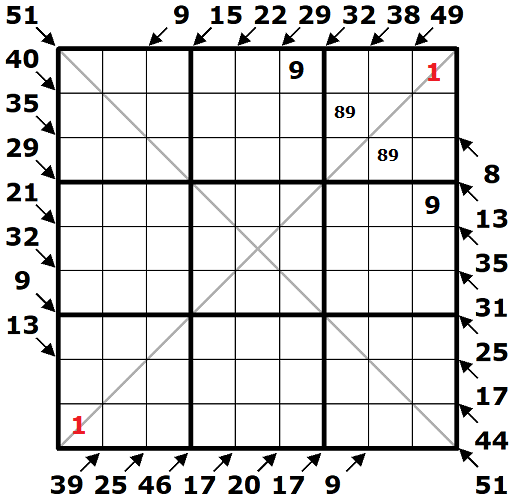
Doplněné jedničky mi umožní rozkrýt rozložení dalších čísel v 3. a 7. čtverci. Ve třetím čtverci dospěju k součtu diagonál činícím 1 + 8 + 13 + 17 = 39 a do 45 mi chybí číslo 6, které doplním na třetí řádek do sedmého sloupce. Číslo 6 spolu s čííslem 1 mi navíc vyloučí dvě možné kombinace součtu 8 na 2-políčkové diagonále, kde mohu doplnit jen čísla 3 a 5, součet 13 budou činit čísla 2, 4 a 7. Na rostoucí diagonále tedy leží 1, 6 a vpisky 2-4-7 pro číslo třetí.
V 7. čtverci mi číslo 1 vyloučí všechny možné kombinace čísla 9 až na 2-3-4. Tím pádem určím pozici pro číslo 6, které musím umístit na rostoucí diagonálu, tedy jedině na sedmý řádek do třetího sloupce. Jediná možná kombinace čísla 13 v této chvíli je 5 a 8 a na 4-políčkovou diagonálu se součtem 32 zbývají v tomto čtverci čísla 7 a 9.
Na rostoucí diagonále leží trojice čísel 1, 6 a jedno z čísel 2 nebo 4, která jsou společná mezi vpiskami v 3. i 7. čtverci. Číslo 7, respektive číslo 3 si mohu ze vpisků na rostoucí diagonále smazat.
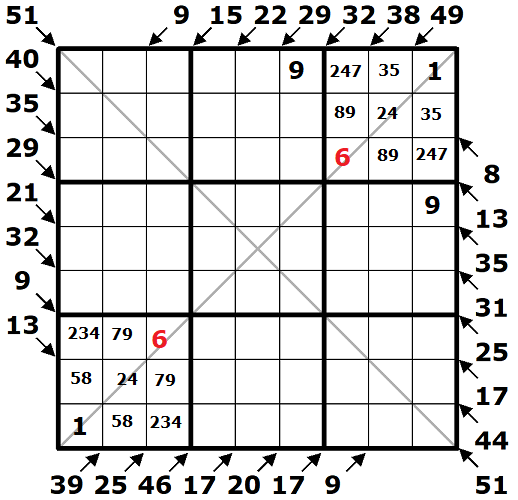
I když neznám přesný součet trojice čísel na rostoucí diagonále, může to být 1 + 2 + 6 = 9 nebo 1 + 4 + 6 = 11, pokusím se vzhledem k množství zadaných čísel kolem tabulky o celkový součet všech diagonál tabulky jdoucí zleva vzhůru vpravo, tedy obdobně jako dřívější součet, za který jsem byl náležitě odměněn dvěmi jedničkami v rozích. Dospěl jsem k součtu 367, do čísla 405 mi zbývá 38. Z tohoto zbytku zkusmo odečtu mi dvě nabízené kombinace rostoucí diagonály, tedy 38 – (3 * 9) = 11 a 38 – (3 * 11) = 5. Díky dvěma jedničkám v rozích bych mohl potencionální součet rohových čísel 5 vytvořit pouze pomocí čísel 2 a 3, což by ale znamenalo, že bych na klesající diagonále musel obě čísla použít, ale tím bych se už nedopídil součtu 17, který je mi od začátku pro klesající diagonálu znám. Součtem levého horního a pravého dolního rohu tedy bude číslo 11 a posledním hledaným číslem rostoucí diagonály bude číslo 2. Chápeme, žejo? ![]()
Pojďme zkusit počítat dále. Nyní znám trojici čísel 126 rostoucí diagonály, celkový součet 17 diagonály klesající, součet dvou čísel klesající diagonály v rozích, tj. 11, a navíc vím, že ve středovém poli tabulky bude číslo společné pro obě hledané trojice a tudíž to musí být jedno z čísel 1, 2 nebo 6. Uff, to musíme dát do kupy! ![]() Na středové číslo v podobě 1 by mi zbyl součet dvojice čísel klesající diagonály 16, tudíž čísla 7 a 9. Z těchto tří čísel 1-7-9 já číslo jedenáct pro rohy nesložím. Na středové číslo v podobě 2 by mi zbyl součet dvojice čísel 15. Při faktu, že nemohu použít číslo 6 (protože by se nacházelo v 5. čtverci jako součást rostoucí diagonály), by mi zbyla čísla 7 a 8. Z trojice čísel 2-7-8 opět nesložím požadovaný součet 11 pro rohová čísla. Ve středovém poli tak bude číslo 6. Zbylá dvě čísla tvoří součet 11, což bude 3-8 nebo 4-7 (2-9 nemohu použít, protože číslo 2 mi zabírá rostoucí diagonála).
Na středové číslo v podobě 1 by mi zbyl součet dvojice čísel klesající diagonály 16, tudíž čísla 7 a 9. Z těchto tří čísel 1-7-9 já číslo jedenáct pro rohy nesložím. Na středové číslo v podobě 2 by mi zbyl součet dvojice čísel 15. Při faktu, že nemohu použít číslo 6 (protože by se nacházelo v 5. čtverci jako součást rostoucí diagonály), by mi zbyla čísla 7 a 8. Z trojice čísel 2-7-8 opět nesložím požadovaný součet 11 pro rohová čísla. Ve středovém poli tak bude číslo 6. Zbylá dvě čísla tvoří součet 11, což bude 3-8 nebo 4-7 (2-9 nemohu použít, protože číslo 2 mi zabírá rostoucí diagonála).
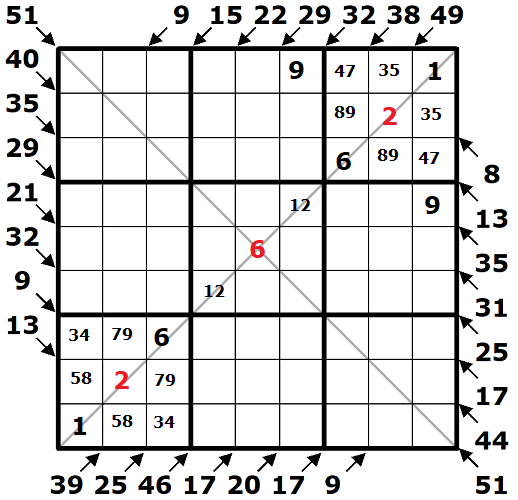
A aby toho počítání nebylo málo, jak lze vytvořit požadovaný součet rohových čísel 11? Pokud bych do rohu umístil číslo 6, tak by v protilehlém rohu muselo být číslo 5, což nelze, do součtu klesající diagonály by mi zbývalo zase 6 a já bych nedospěl k trojici různých čísel pro klesající diagonálu. Šestka tedy nebude v rohu a co čert nechtěl, já ji pomocí technik klasického sudoku doplním do zbytku tabulky.
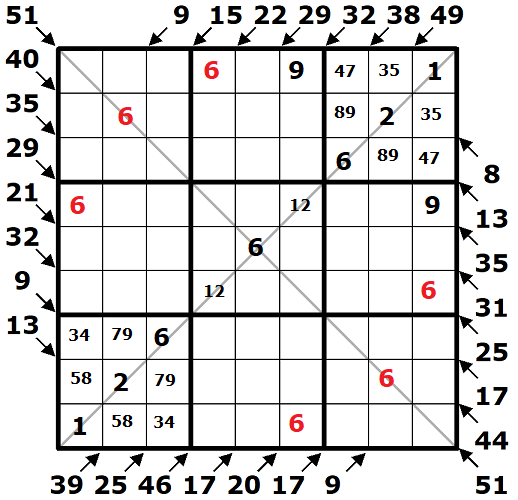
Klíčem k doluštění tabulky bude určení čísel klesající diagonály. Pro 2-políčkové diagonály v rozích 1. a 9. čtverce se součtem 9 nemohu použít čísla 6, 2 ani 1, tvoří je tak čísla 4 a 5. A mám to. ![]() Na klesající diagonále spolu s číslem 6 leží čísla 3 a 8 (kombinaci čísel 4-7 jsem právě vyloučil použitím čísla 4 mimo klesající diagonálu). V 1. čtverci potřebuji dopočítat 4-políčkovou diagonálu, kde dvojici šestek doplním číslem 9, které nemohu doplnit do jiného součtu, a k němu doplním číslo 1. Do součtu 15 mi zbývá 2 a 7. V 9. čtverci mi 4-políčkový součet 20 vytvoří pouze čísla 1 a 7 a do 17 nacpu 2 a 9.
Na klesající diagonále spolu s číslem 6 leží čísla 3 a 8 (kombinaci čísel 4-7 jsem právě vyloučil použitím čísla 4 mimo klesající diagonálu). V 1. čtverci potřebuji dopočítat 4-políčkovou diagonálu, kde dvojici šestek doplním číslem 9, které nemohu doplnit do jiného součtu, a k němu doplním číslo 1. Do součtu 15 mi zbývá 2 a 7. V 9. čtverci mi 4-políčkový součet 20 vytvoří pouze čísla 1 a 7 a do 17 nacpu 2 a 9.
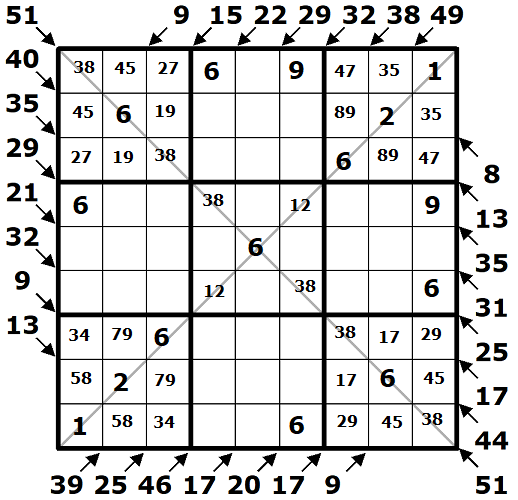
Už mám počítání a všemožných kombinací po krk, pojďme doluštit tabulku klasicky. V 9. sloupci mi číslo 9 rozlouskne devítky v 9. čtverci a rozjede spirálu, která mi určí všechny čísla 1., 3, 7. a 9. čtverce.
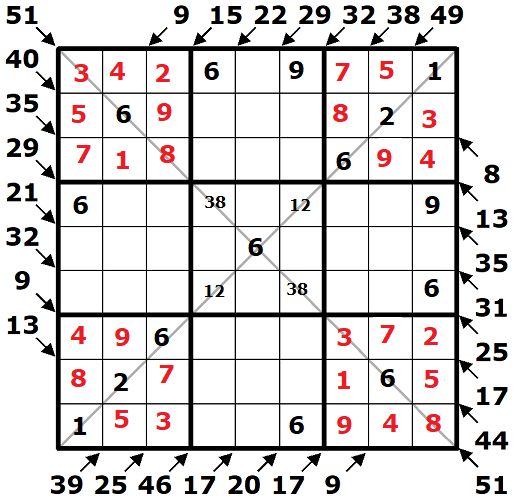
A teď už je to jen o součtech zabijáčka a s tím si hravě poradíte. Co na úlohu říkáte? ![]() Kdyby se toto objevilo na turnaji, byla by to od autora pěkná lumpárna, v dlouhodobé soutěži je spíše čas bádat nad tabulkami.
Kdyby se toto objevilo na turnaji, byla by to od autora pěkná lumpárna, v dlouhodobé soutěži je spíše čas bádat nad tabulkami.
V případě kombinace více variant sudoku doporučuji vyždímat ze sebe co jde, k uvědomění si, co vše tabulka nabízí. Donutit hledat hráče něco nového přitom nemusí být ani autorův záměr. A pokud objevíte svůj originální postup řešení, buďte na sebe náležitě pyšní.
sepsal Pavel Kadlečík
Theme by Danetsoft and Danang Probo Sayekti inspired by Maksimer