Úloha Hanidoku z 381 kola dlouhodobé soutěže vzbudila lehký rozruch 
, tento návod vám doufám poradí, jak úlohu řešit. Upozorňuji, že uvedený postup rozhodně nemusí být optimální. Za každý další alternativní budu rád a je možnost ho i následně připojit k tomuto textu.
Hanidoku
Doplňte do všech prázdných políček čísla 1-9 tak, aby se v žádném ze tří směrů šestiúhelníkového pole čísla neopakovala a zároveň se v každém směru nacházely pouze skupiny sousledných čísel.
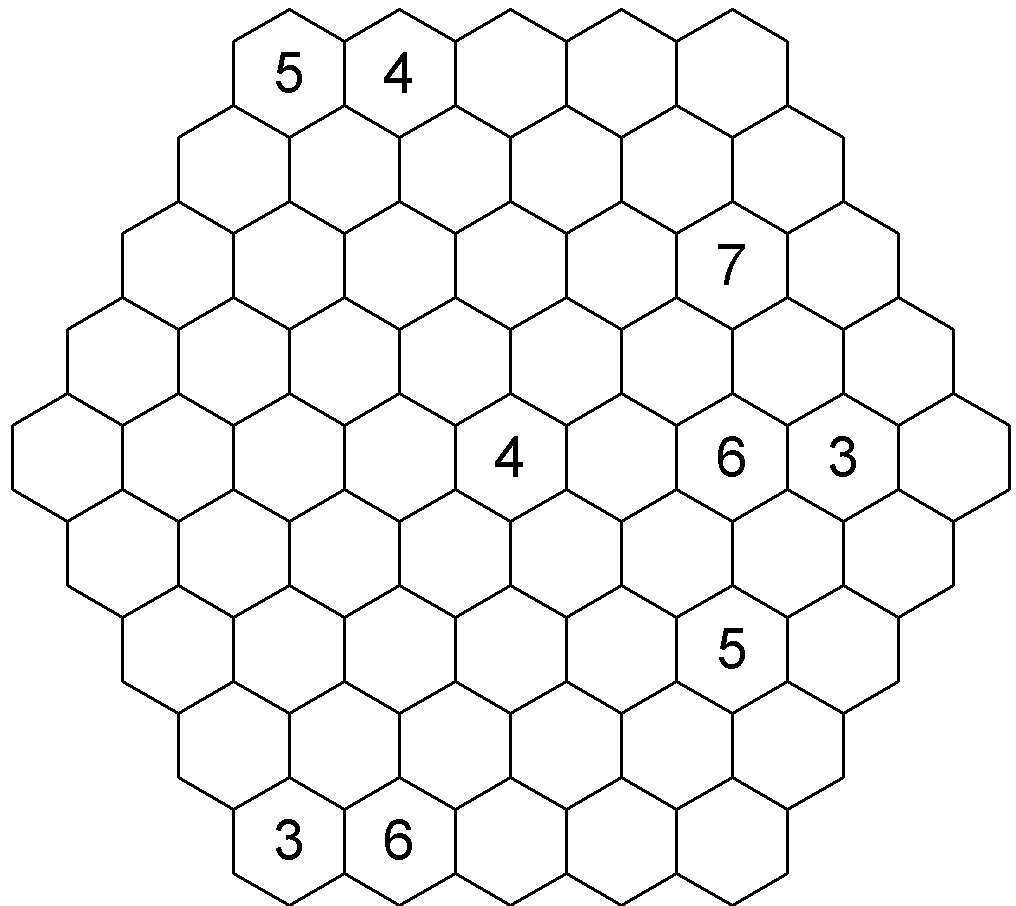
Nejprve bych si označil směry, jak je budu v textu nazývat, jelikož v šestiúhelníkovém poli to není moc zajeté. Možná to bude trochu kostrbaté, snad mi odpustíte. První směr, vodorovný, budu nazývat řádky, tím jsem vás určitě překvapil 
, pozice budu počítat zleva doprava. Tudíž na prvním řádku na první pozici je číslo 5, na druhé pozici je číslo 4 a například na třetím řádku je číslo 7 na pozici šesté. Směr druhý, na který se mohu koukat zleva směrem doprava dolů budu nazývat levými „diagonálami“, počítat je odleva a pozice polí budu počítat směrem dolů. Tudíž na první levé diagonále se nachází číslo 3 na páté pozici, na druhé levé diagonále číslo 6 na šesté pozici. Třetí směr budou pravé „diagonály“. Budu je počítat též odleva. Jejich pozice počítám odspodu nahoru. Takže na první pravé diagonále se nachází číslo 5 na páté pozici, na druhé pravé diagonále číslo 4 na šesté pozici a například na sedmé pravé diagonále je číslo 6 na pozici páté.
Pojďme k věcem, které je vhodné (či pro komfortnější řešení úlohy nutné) si uvědomit. Připojuji obrázek všech levých diagonál. Pro oba další směry platí totéž. Na koncích linií jsou uvedena čísla, která se v daném směru musí vyskytovat. Ve všech skupinách o 5 polích musí být číslo 5 (příkladem takové skupiny čísel bude 1, 3, 2, 4, 5 nebo 8, 5, 6, 7, 9). Ve skupinách o 6 polích musí být určitě čísla 4, 5, 6, ve skupinách o 7 polích čísla 3, 4, 5, 6, 7, o 8 polích čísla 2-8, až dojdeme ke skupinám o 9 políčkách, kde se nacházejí čísla 1-9 každé jednou. Z toho vídím, že čím početnější skupina polí, tím se více pro mě vyloupne čísel, o kterých vím, že v tomto směru budou. V zadání není moc čísel uvedeno, takže začít tabulku tím, že si budu psát do políček o osmi či devíti polích všechny možné čísla, pak by se úloha mohla stát nepřehlednou.
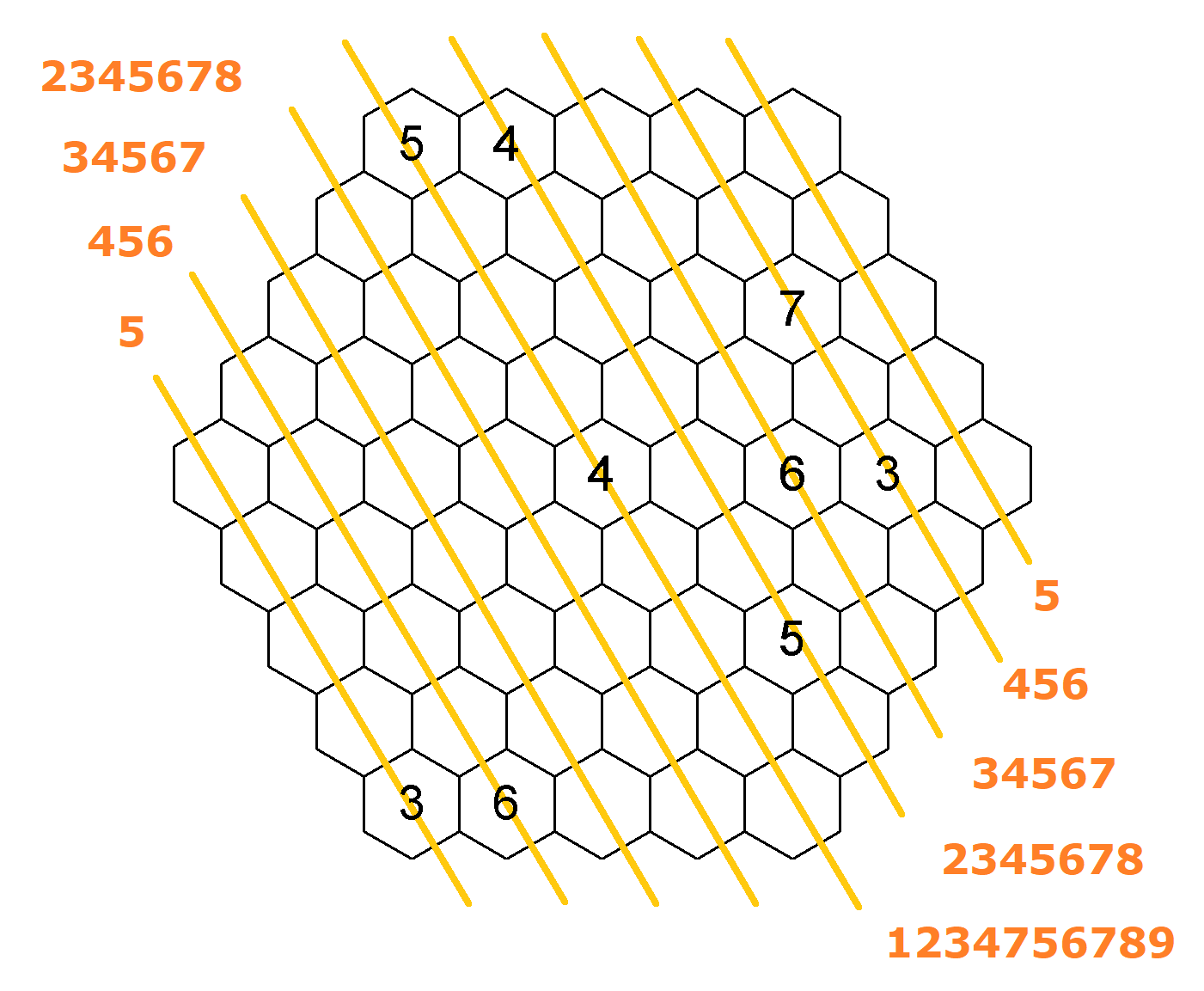
Z tohoto rozboru si odvozuji, že pokud se některé z čísel vyskytuje v obrazci vícekrát a zároveň znám směr, kde musí být, tak by mohlo být fajn mu věnovat pozornost. Pokusím se tedy doplňovat čísla postupně od 5, dále číslo 4 nebo 6, pak 3 nebo 7 atd. Přesná četnost čísel v obrazci mi není předem známa s výjimkou čísla 5. Pro optimální postup řešení též záleží, jaká čísla jsou již zadána. Dále bych se v mém plánu zaměřil na směry o méně polích, kde je šance, že čísla doplním snáze (je tu méně možností), případně moje vpisky nebudou o mnoho číslech. Není nutné se svého plánu držet na 100 %, ale je šikovné mít takovou linku, ke které se budu případně vracet, kdybych nevěděl jak dál.
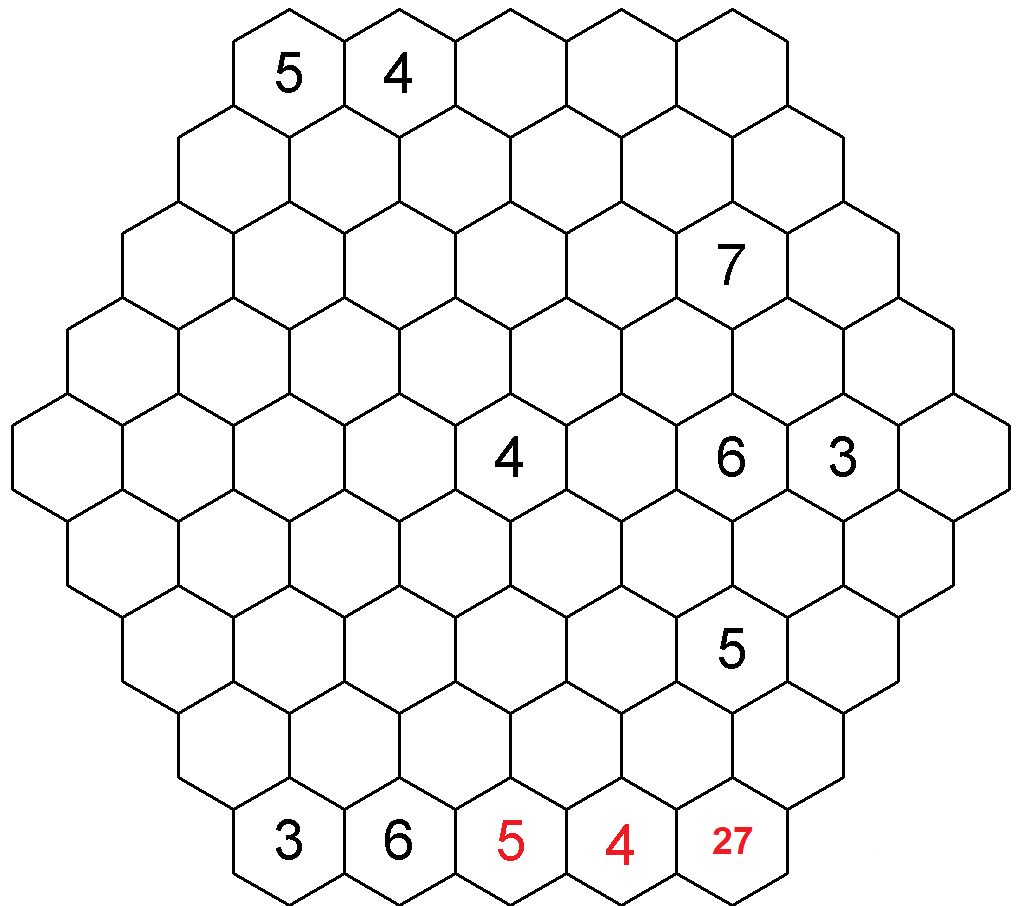
Začněme luštit. Nejprve jsem si všiml směrů, kde jsou již doplněna čísla a tato si jsou hodnotově vzdálena. Co tím myslím? V devátém řádku mám čísla 6 a 3, tudíž vím, že určitě tu budou čísla 4 a 5, plus jedno další číslo, buď 2 nebo 7. Na osmé levé diagonále jsou zadána čísla 7 a 3, tudíž v tomto směru o 6 políčkách budou čísla 4, 5 a 6 (což z pravidel o šestipolíčkových směrech vím stejně) a jedno další číslo, buď 2 nebo 8.
U devátého řádku mi dvě zadané pětky v úloze vyblokovávají pozici čtvrtou a pátou, číslo 5 tedy dopíši na pozici třetí na devátém řádku. Pak mohu doplnit i číslo 4 na pozici čtvrtou, jelikož pátá pozice je atakována již zadanou čtyřkou. Na pozici pátou doplním dvopisek 27. Obdobně bych se zkusil podívat na zmíněnou osmou levou diagonálu, ale nelze určit nyní žádné číslo, pouze, že číslo 5 bude na druhé či šesté pozici a číslo 4 na pozici čtvrté ši šesté. Tím jsem v tabulce zaplnil, co je jisté na první pohled. Vrátím se tedy k mé lince, že v každém směru tabulky musí být číslo 5.
Pro názornost si zabarvím všechna pole tabulky, kde jsou již doplněna čísla, a pak si ze všech čísel 5 nakreslím tykadélka, abych věděl, v kterých políčkách již číslo 5 být nemůže. Zbylo mi 16 bílých políček, do kterých musím doplnit číslo 5 šestkrát.
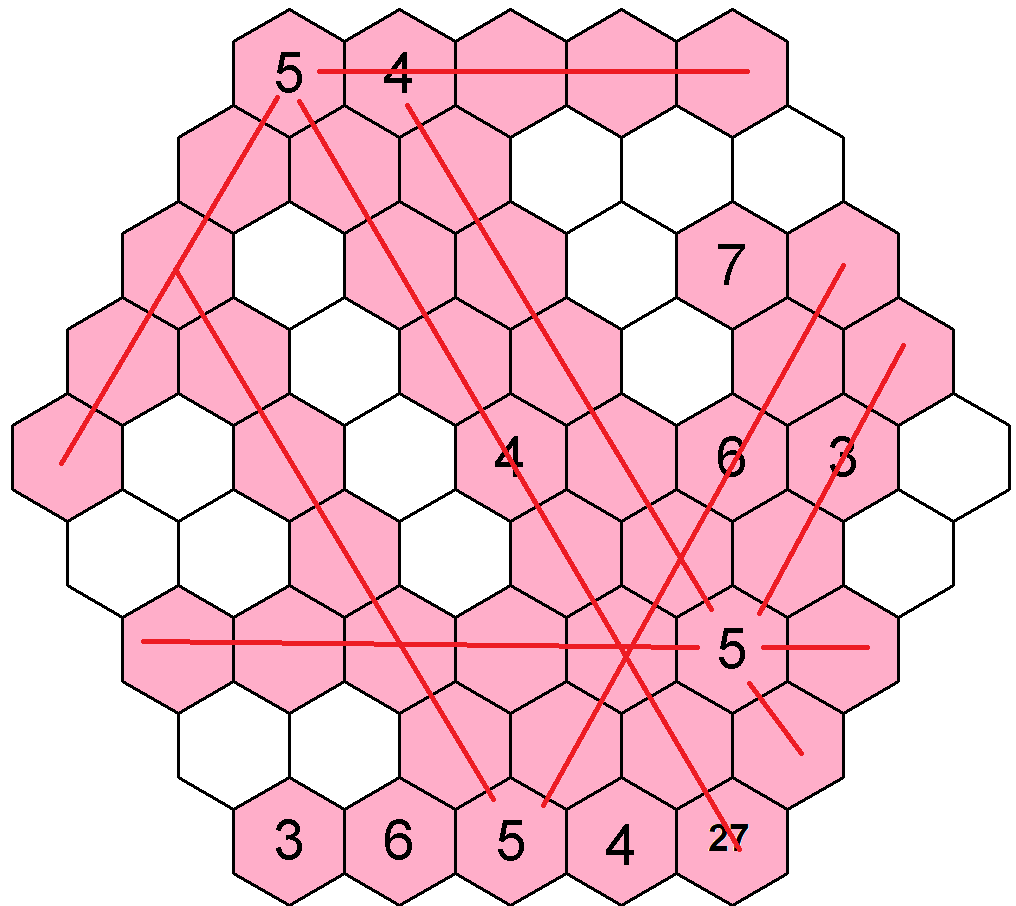
Když kouknu na třetí a čtvrtý řádek, objeví se přede mnou trik číslo jedna. Oba řádky musí obsahovat číslo 5, přitom mám pouze dvě volná pole v obou řádcích, konkrétně na třetím řádku pozici druhou a pátou, na čtvrtém řádku pozici třetí a šestou, kam mohu doplnit číslo 5. Co to znamená? Nevím na jakých pozicích se přesně číslo 5 bude nacházet ze dvou variant na třetím a čtvrtém řádku, ale vím jistě, že tam bude. Mohu si pole označit a zároveň vyloučit výskyt čísla 5 na ostatních polích čtvrté levé diagonály a sedmé levé diagonály (konkrétně to je pozice čtvrtá na druhém řádku, na pátém řádku a šestém řádku).
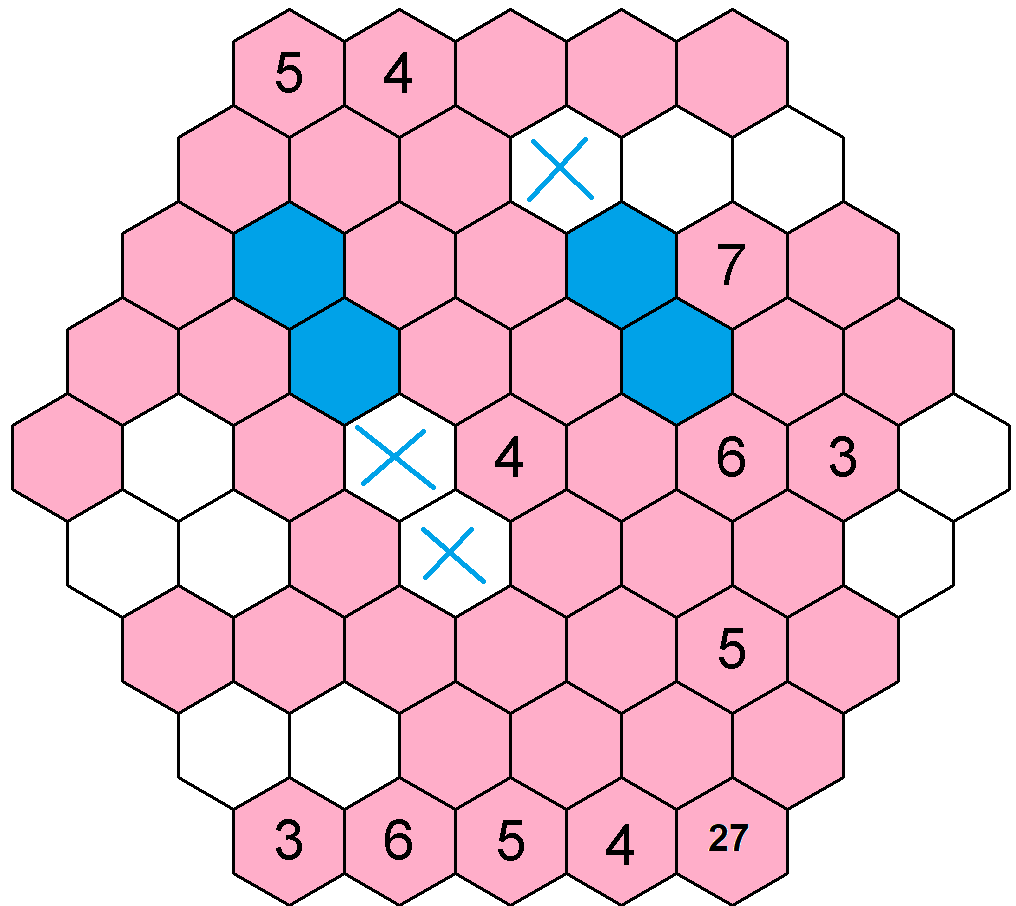
Čtvrtá pozice na druhém řádku šla vyloučit obdobnou úvahou pro osmou a devátou levou diagonálu, kdy jsou pro výskyt čísla 5 též jen dvě možnosti na obou diagonálách.
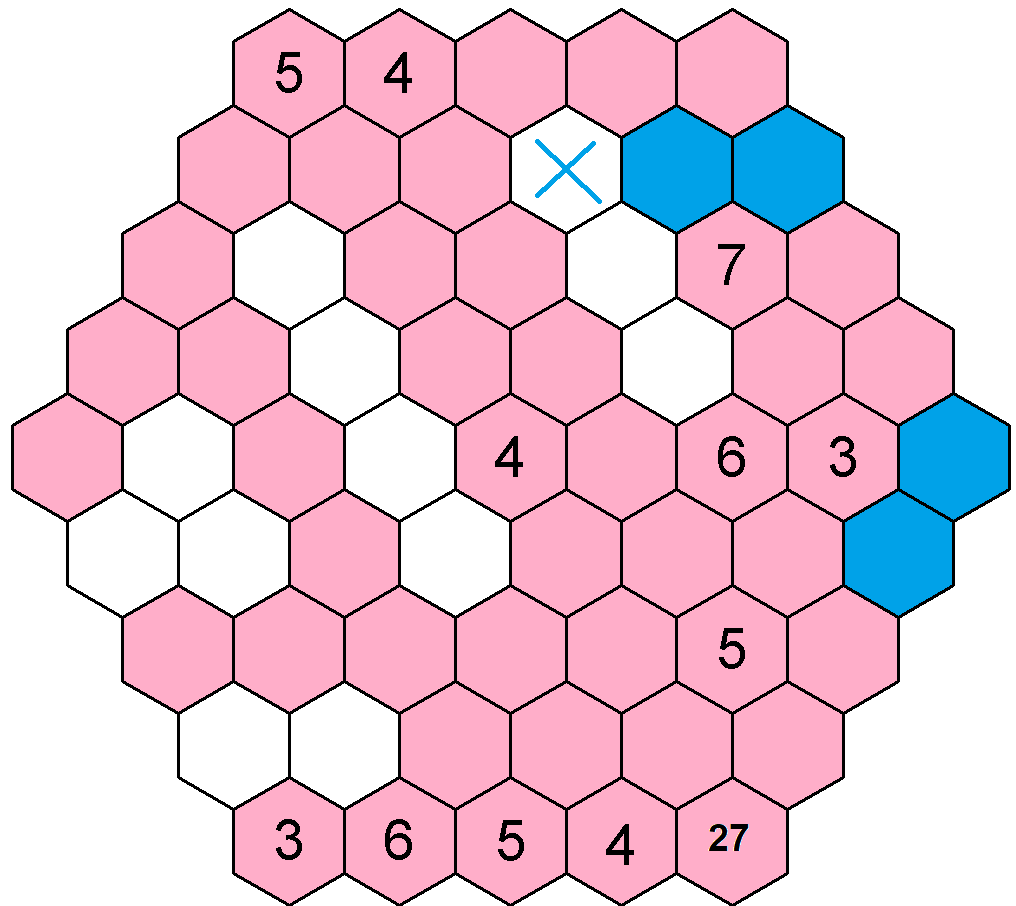
Pojďme dále a využijme toho, že jsme odebrali některá pole, kde být číslo 5 nemůže. Na čtvrté pravé diagonále nám těmito kroky zbylo pouze jedno volné pole pro číslo 5 na první pozici. Mohu tedy doplnit číslo 5 (na osmý řádek první pozici). Alternativním způsobem, jak určit tuto pětku je, pokud využijeme námi určené dvojičky (vyobrazené krátkou čárou), konkrétně dvojičku na druhém řádku a dvojičku na sedmé levé diagonále. Obě dvojičky nám určují, kde v těchto dvou směrech bude číslo 5, ať už bude na jedné či druhé pozici ve směru jednom, určí nám to následně pozici čísla 5 ve směru druhém. Takže stejně jako ve dvou předchozích případech této metody, můžeme vyloučit ostatní čísla na páté a šesté pravé diagonále, kde se dvojička nachází. Konkrétně je to pouze jedno pole a to druhá pozice na osmém řádku. Z toho mi zbyde už jen jedna možnost, kam umístit číslo 5 na osmém řádku a to první pozice.
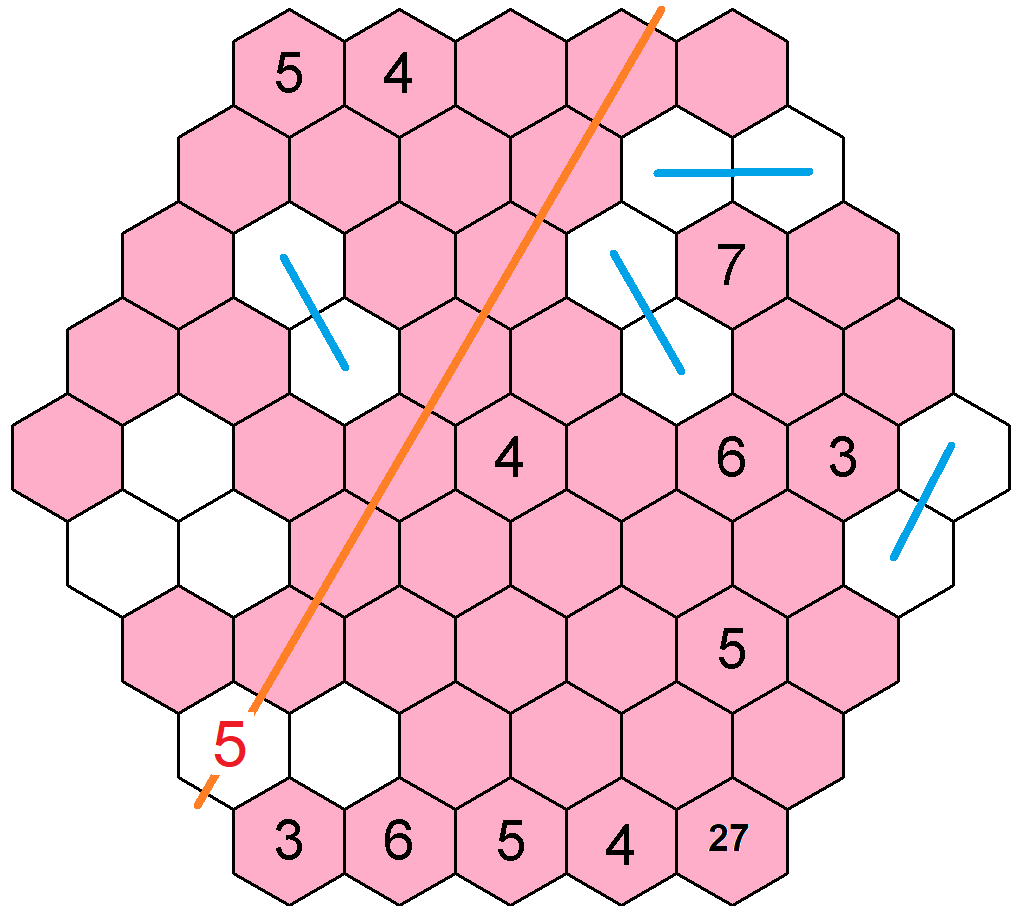
Doplněná pětka mi omezí další pole na první levé diagonále a utvoří poslední pomyslnu dvojičku čísel 5 na druhé levé diagonále. Doplnění zbylých pěti čísel 5 v obrazci má dvě řešení, musíme tedy pokračovat dále s dalšími čísly.
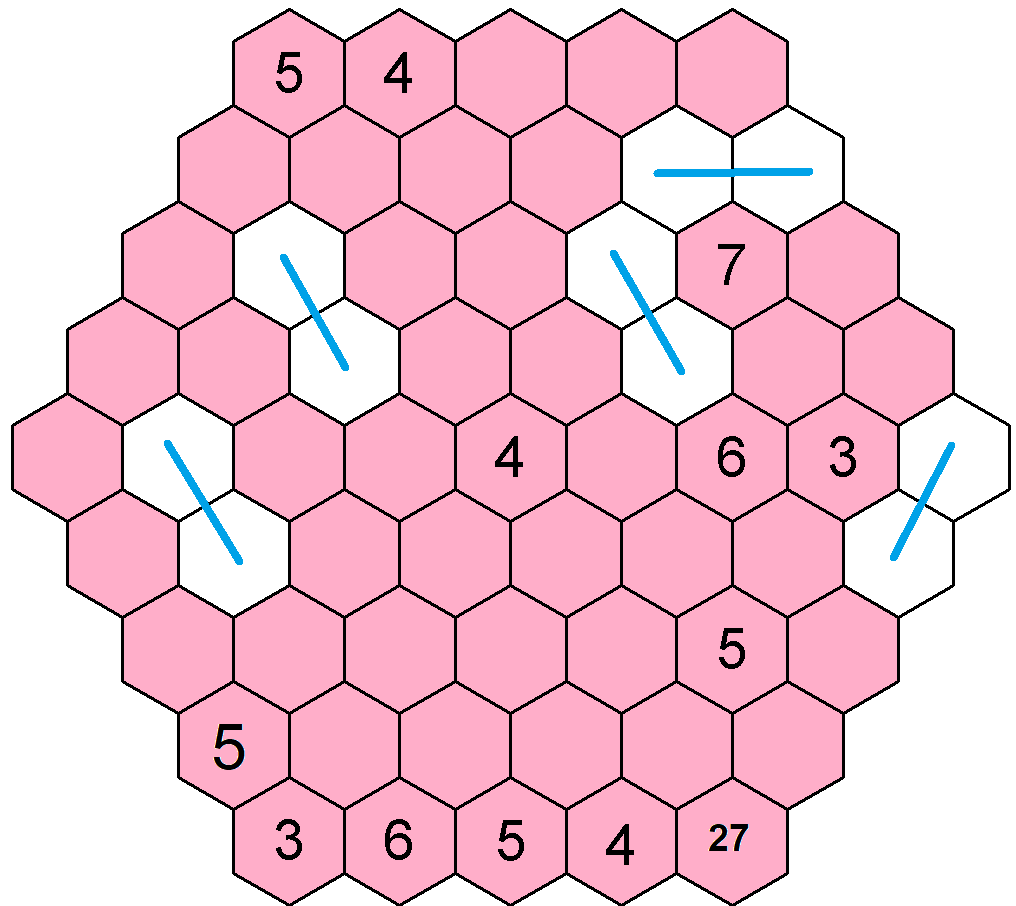
Abychom si prosvištěli tuto metodu, zkusíme to samé udělat s číslem 4. A aby to bylo názornější (a zábavnější ), umazal jsem si právě doplněnou pětku. Takto bych normálně nepostupoval, ale všiml jsem si toho při tvorbě tohoto postupu, tak proč to neukázat. Opět si obarvím všechna již doplněná čísla a z čísel 4 nakreslím tykadélka, kde být toto číslo nemůže.
Zaujal mě druhý a osmý řádek. Na těchto dvou řádcích lze doplnit číslo 4 pouze na dvě pozice, konkrétně na druhém řádku na pozici čtvrtou a šestou, na osmém řádku na pozici první a třetí. Co je ale zajímavé, že tyto dvojičky se nacházejí na stejných pravých diagonálách, konkrétně na čtvrté a šesté. Doplnění čísla 4 na druhém a osmén řádku má sice dvě varianty, jak to udělat, mohu ale alespoň umazat ze čtvrté a šesté diagonály jiná potenciální pole pro čísla 4. Na nich číslo 4 být nemůže, poněvadž bych pak nebyl schopen doplnit číslo 4 jak na druhý, tak i na osmý řádek.
Umazání možností pro umístění čísla 4 mi vykrystalizuje ve vznik dvojiček na třetím a čtvrtém řádku, dále pak na šestém a sedmém řádku. Z možného rozmístění čísla 4 v obrazci vidím, že jsou dvě varianty, jak to provést. Dokonce je rozmístění čísla 4 symetrické podle středu tabulky, což ale jinak pro naše řešení není podstatné.
Příjemnou věcí je, že jedna možnost, kam dosadit číslo 4, je již zaplněna číslem 5, které jsem si v předešlém kroku sebemrskačsky odebral. Pokud tedy číslo 5 doplním na osmý řádek první pozici, rázem mi vypadnou všechny 4 v obrazci.
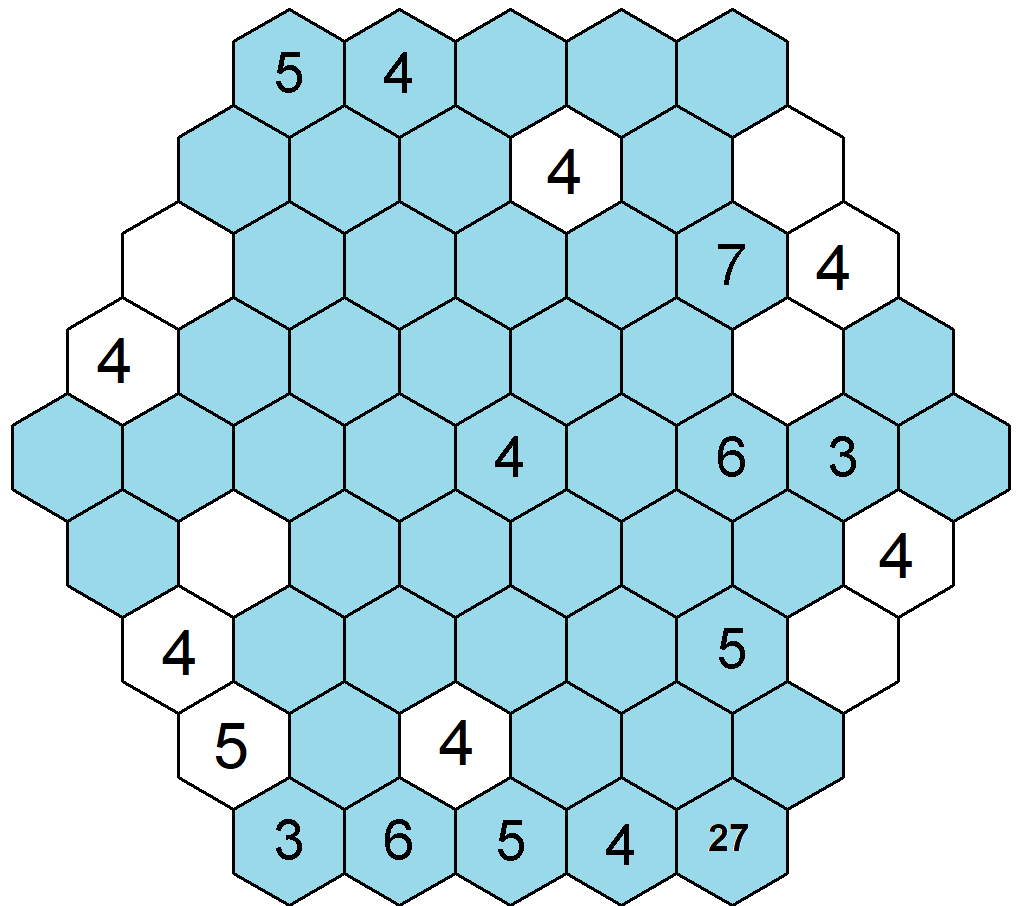
Co čert chtěl, doplněním čtyřek do obrazce jsme zároveň zaplnili jedno pole, kde se vyskytovala možnost pro doplnění čásla 5. Tím pádem je následně možno doplnit zbylá čísla 5 do obrazce. Pro vysvětlenou dodávám, že do tohoto stavu bychom se dostali i bez názorné ukázky s číslem 4 a odebranou pětkou. Jedna doplněná pětka by nám omezila doplňování čísla 4, pak bychom krok po krůčku dospěli ke všem čtyřkám, na což by nám měl zasvítit radar, proč bychom se nevrátili k původní lince, jak tuto úlohu luštit, a doplnili bychom všechna čísla 5.
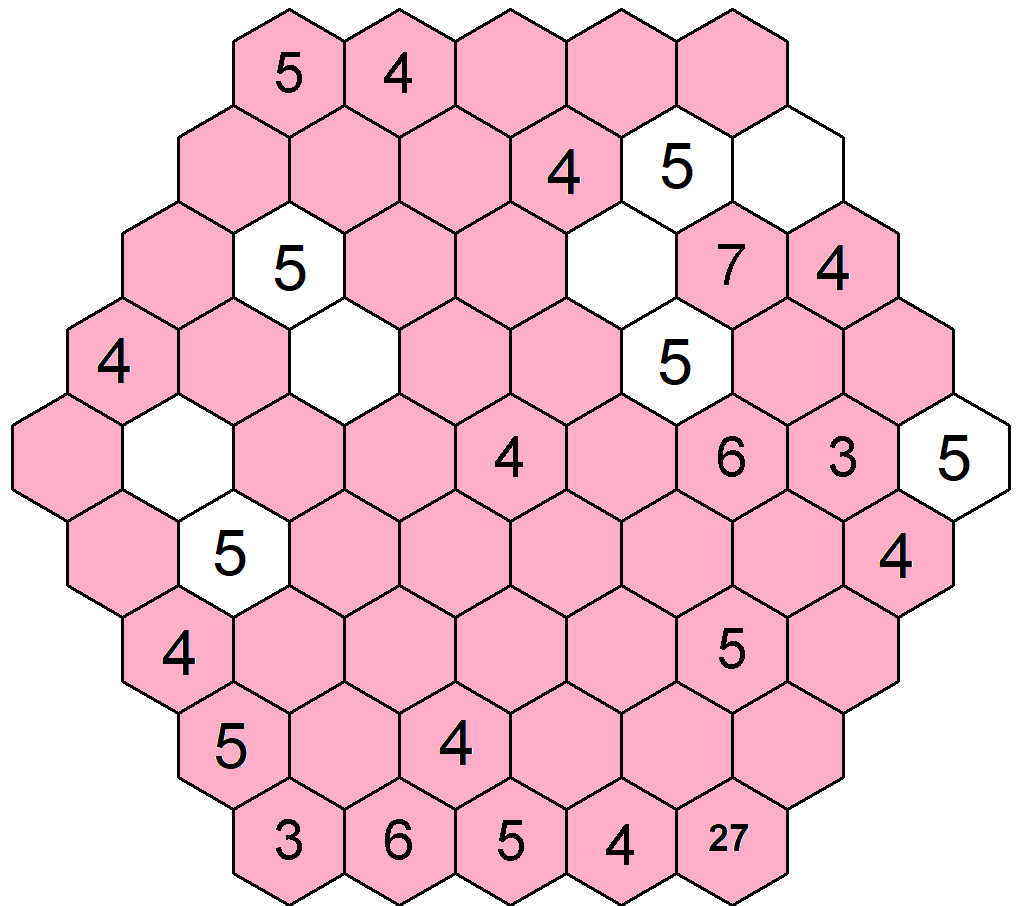
Náš plán nám říká, že dalším nejčetnějším číslem by mohlo být číslo 6, které se na tuty vyskytuje ve všech směrech o 6 a více políčkách. Ve směrech s pěti políčky nám tato informace není známa.
Na osmé pravé diagonále jsem vzýval číslo 6 již na začátku mého postupu, nyní po doplnění čísel 4 a 5 zbývá již jediné volné pole. Doplním tedy šestku na první řádek na čtvrtou pozici. V obrazci začínají přibývat šestky, vystrčím tedy tykadélka směrem dolů z šestky na pátém řádku, stejnětak nahoru z šestky na devátém řádku. Na sedmém řádku nám zbyde pro šestku pouze třetí pozice, tak ji tam doplním. Tuto šestku hned využiji a vystrčím z ní tykadla na šestý řádek, kam doplním číslo 6 na pozici první.
Přecházím k metodě "trojúhelníků", kterou jsem už lehce naťukl tykadélky. Techniku lze využít v diagonálním sudoku, samozřejmě v isosudoku, může být použitelná v nepravidelném sudoku a dalších logických úlohách. Aby to bylo názornější, opět si vybarvím pole, kde již nemohu umístit číslo 6.
Trojúhelníky si pro názornost budu zakreslovat přímo do obrazce. Číslo 6 na čtvtém řádku třetí pozici by mi atakovalo obě možné pozice na druhém řádku, z čehož vím, že tam šestka ležet nebude.
(Mohl bych použít předešlou metodu příkladem, že na páté a šesté levé diagonále jsou pouze dvě pozice pro šestku a zároveň vím, že tam být šestka musí. Pak mi tyto dvojičky vyloučí třetí pozici na čtvrtém řádku. A šestka bude na osmé pozici ve čtvrtém řádku.)
Následně doplním ostatní chybějící šestky.
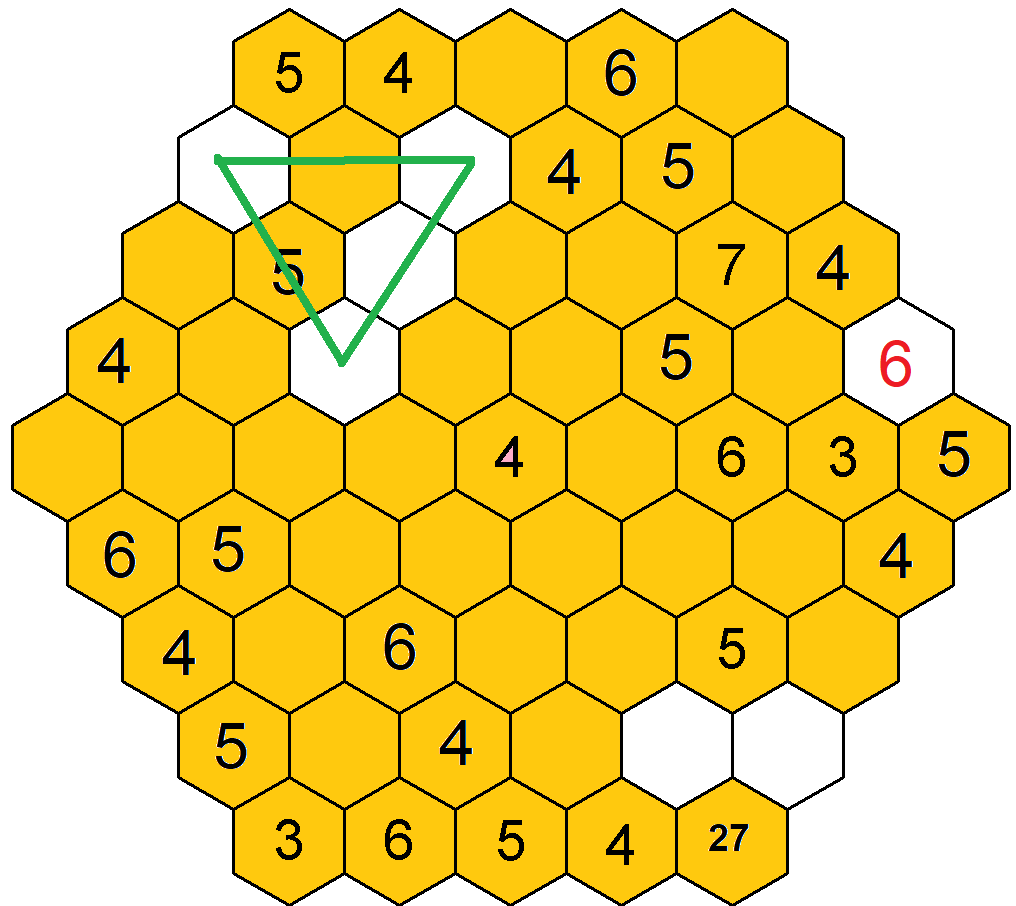
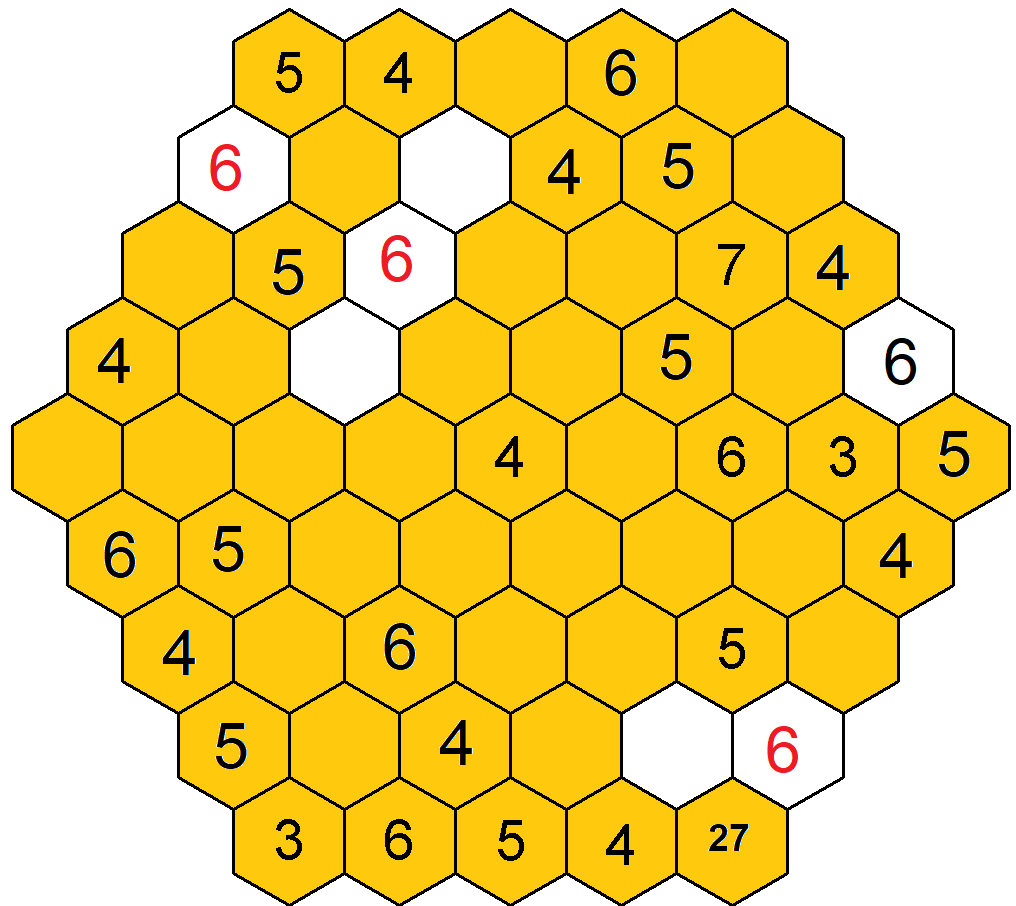
Dále se zkusím věnovat buď trojkám nebo sedmičkám. Trojky jsou zadány dvě, tak zkusím je. Opět si obarvím políčka s již vepsanými čísly, a na to vybarvím všechna pole, kde je výskyt trojek omezen díky jejích zadanýi kamarádům. Zkusím najít opět potencionální trojúhelník, který by mi zredukoval možnosti doplnění trojek. Nejdříve jsem si všimnul třetí pozice na šestém řádku. Pokud bych zde doplnil trojku, již nemohu doplnit číslo 3 na třetí řádek, dva vrcholy trojúhelníku by toto neumožnily. Na šestém řádku na třetí pozici tedy trojka být nemůže. Toho využiji a mohu nakreslit další trojúhelník, který mi řekne, že na sedmém řádku páté pozici nemůže být taktéž číslo 3, jelikož by následně znemožnilo dopsání trojky na šestý řádek.
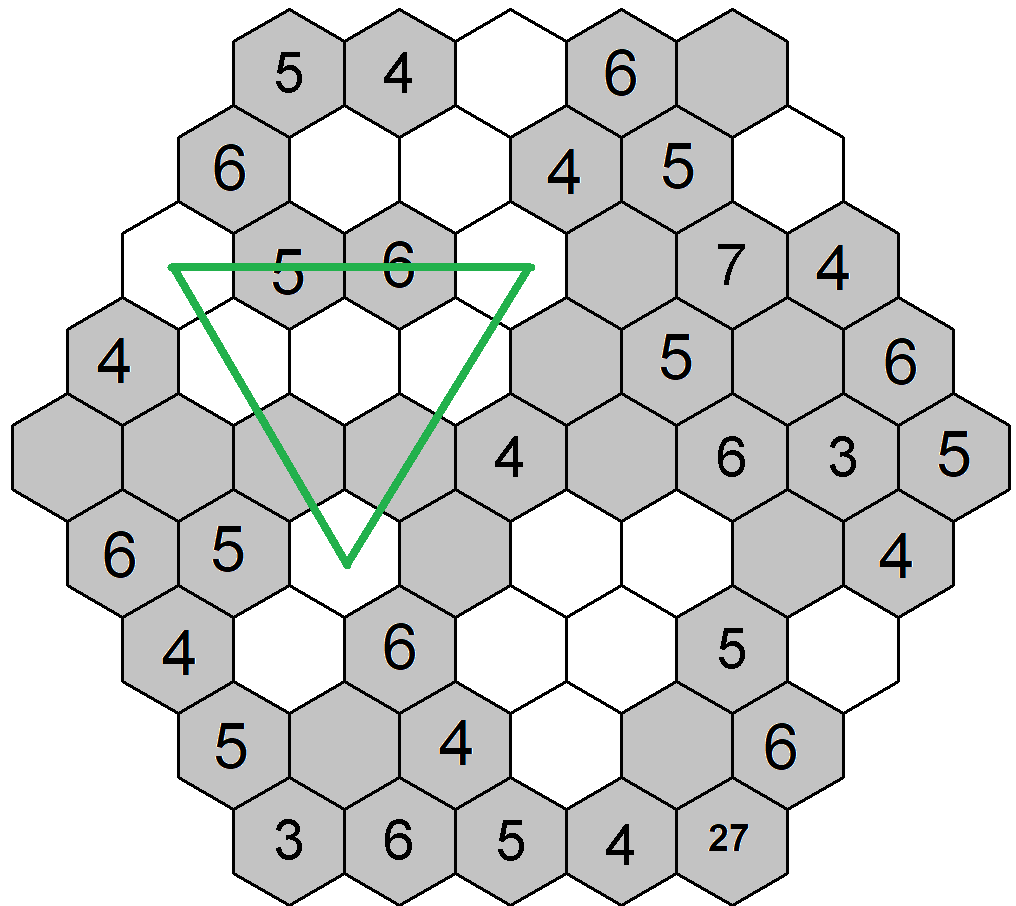
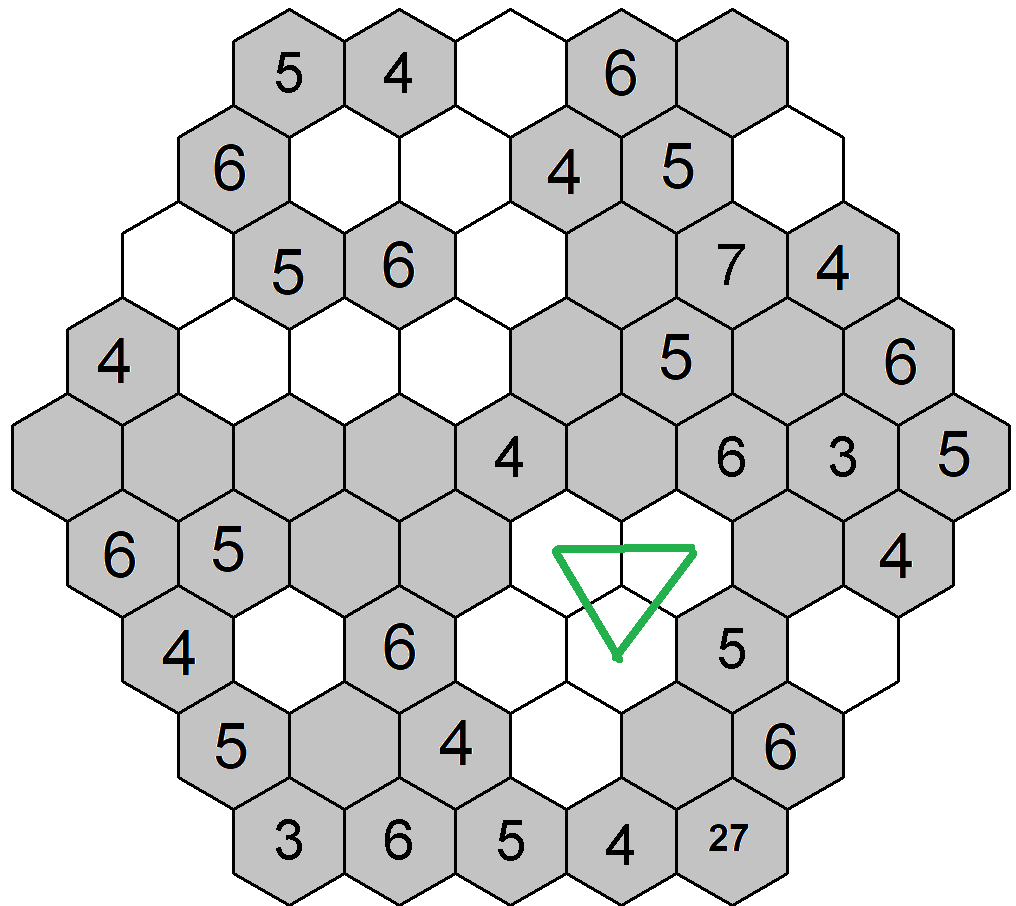
Koukám dále, ale žádné další trojúhelníky nevidím. Přijde mi, že už je nejvyšší čas si doplnit nějaké vpisky. Na první levé diagonále na první pozici nám chybí poslední číslo do řady 3-6, což tedy může být pouze 2 nebo 7. Tím pádem na první pravou diagonálu na pozici třetí můžeme dopsat k již zadaným číslům 4-6, pouze čísla 3 nebo 8. Pokud by na pozici první bylo číslo 2, pak je na třetí pozici bude číslo 3, pokud bude na první pozici číslo 7, bude na třetí pozici 3 nebo 8. Takže proto. Na osmé levé diagonále nám chybí v řadě 3-7 též jedno číslo, pak tedy na zbylém poli bude 2 nebo 8. Zajímavá je devátá levá diagonála, kde mám čísla 4-6 a chybí dvě doplnit. První pozice je atakována trojkou, takže pokud by v řadě bylo číslo 3, může být pouze na pozici druhé. Druhá pozice je pro změnu atakována číslem 7, tudíž pokud v řadě bude sedmička může být pouze na první pozici. Z toho plyne, při doplnění sedmičky bude na druhé pozici 3 nebo 8, při doplnění 3 bude na první pozici 2 nebo 7. Doplnění obou čísel 3 i 7 do této řady máme vpisky již pokryto. Vpiskujeme dále, v první řadě máme čísla 4-6, pak vpisku 27 a volné pole. Ve volném poli může být pouze 3 nebo 8 viz první pravá diagonála, kde jsme si tuto situaci již zkusili. Obdobný případ bude devátá pravá diagonála, kde zase máme čísla 4-6 a vpisku 27, což nám obdobně pro poslední volné pole vyhotoví vpisky 3 a 8. Je to furt ten stejný systém, kdy mohu mít řady 2-6 nebo 3-7 nebo 4-8, pokud doplním číslo 2, musím mít i číslo 3, pokud doplním číslo 8, musím mít i číslo 7, v poslední variantě bude doplněno číslo 3 a číslo 7. Tímto vpiskováním jsme docílili zajímavého kroku na sedmé levé diagonále o 7 polích, kde jsou čísla 4-6, nově dva dvojpisky 3 a 8, což znamená že na jednom ze dvou volných polí bude číslo 7 a druhé zatím neznáme. Třetí pozici levé diagonály nám jediná zadaná sedmička v obrazci atakuje, číslo 7 doplníme na šestou pozici levé diagonály. Super. Mohu si ještě doplnit vpisky do zbylého pole sedmé levé diagonály, tj. 29. A do volného pole osmé pravé diagonály vpisky 28.
Jelikož jsem doplnil druhou sedmičku a nyní to mám s trojkami fifty fifty, napadla mě trochu bizarní věc pro účely tohoto návodu a tak si vedle obrazce se zabarvenými poli, kde nemůže být trojka, dám obrazec další, kde naopak nemůže být sedmička. Nyní budu hledat trojúhelníky ze sedmiček.
První trojúhelník se vztahuje k sedmému řádku, kde musí být číslo sedm a dvě jeho možné pozice by vyblokovávala sedmička na čtvrtém řádku čtvrté pozici. Další trojúhelník se vztahuje k šesté levé diagonále, která též musí obsahovat číslo 7 a to by znemožnila případná sedmička na čtvrté levé diagonále pozici třetí. A máme tu další trojúhelník vztahující se ke čtvrté pravé diagonále, určující, že číslo 7 nebude na druhé pravé diagonále druhé pozici.
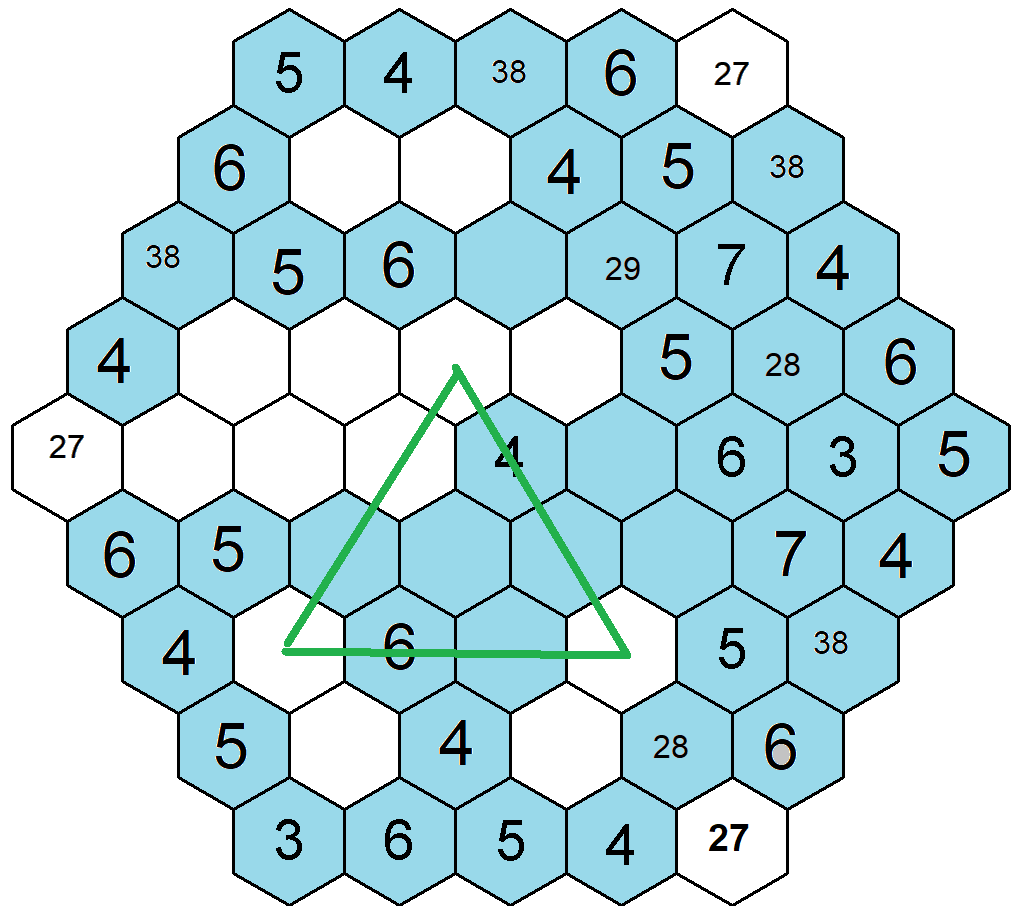
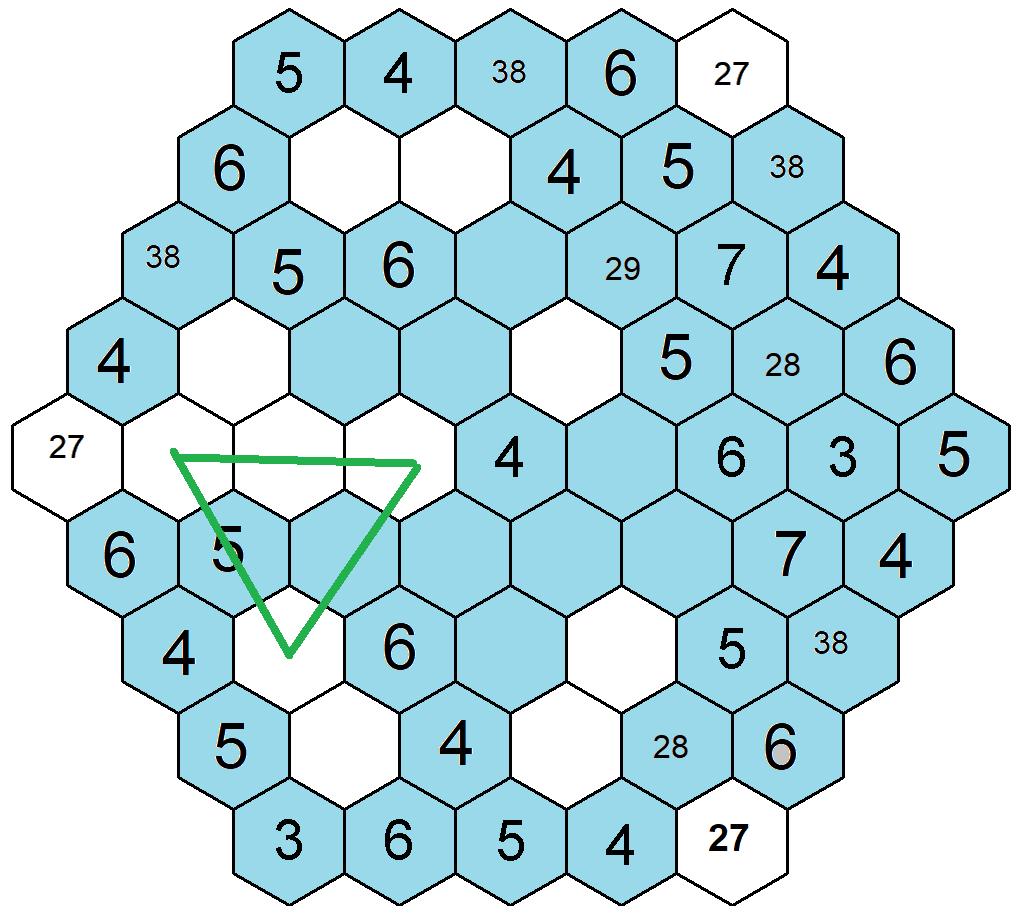
Došly mi náboje s trojúhelníky. tak bych přešel k poslednímu způsobu, jak budu úlohu řešit. Sledovat skupiny polí, pokud možno se soustředit na jejich průsečíky. Efektivní je to spíše pro kratší skupiny polí a odlehlejší hodnoty. Pokud příkladem doplním 9 na průsečík dvou pětipolíčkových skupin, musím na obou z nich utvořit skupinu 5-9, což nemusí být vždy samozřejmé. Pro jednotlivé skupiny polí se budu soustředit na čísla, která v nich musí být obsažena, a dále na ty, která v nich být nesmí.
Zkusím doplnit vpisky. Na osmém řádku mi mohou vzniknout skupiny čísel 1-6 nebo 2-7 nebo 3-8 nebo 4-9. Pole, kde můžu doplnit číslo 3 a kde číslo 7 mi zúží vpisky, konkrétné na druhé pozici na 179, na čtvrté na 379. Zkusím doplnit druhou levou diagonálu, možné skupiny čísel jsou stejné jako v předešlém případě a doplním na druhou pozici druhé levé diagonály vpisky 289, na čtvrtou pak 3789.
Vysvětlivky k obrázku: Pole, kde se mohou vyskytnout čísla 3 (vlevo) a 7 (vpravo) nejsou podbarvena. Šedě jsou označena pole, kde číslo 3 být nemůže, modře pak pole, kde nemůže být číslo 7.
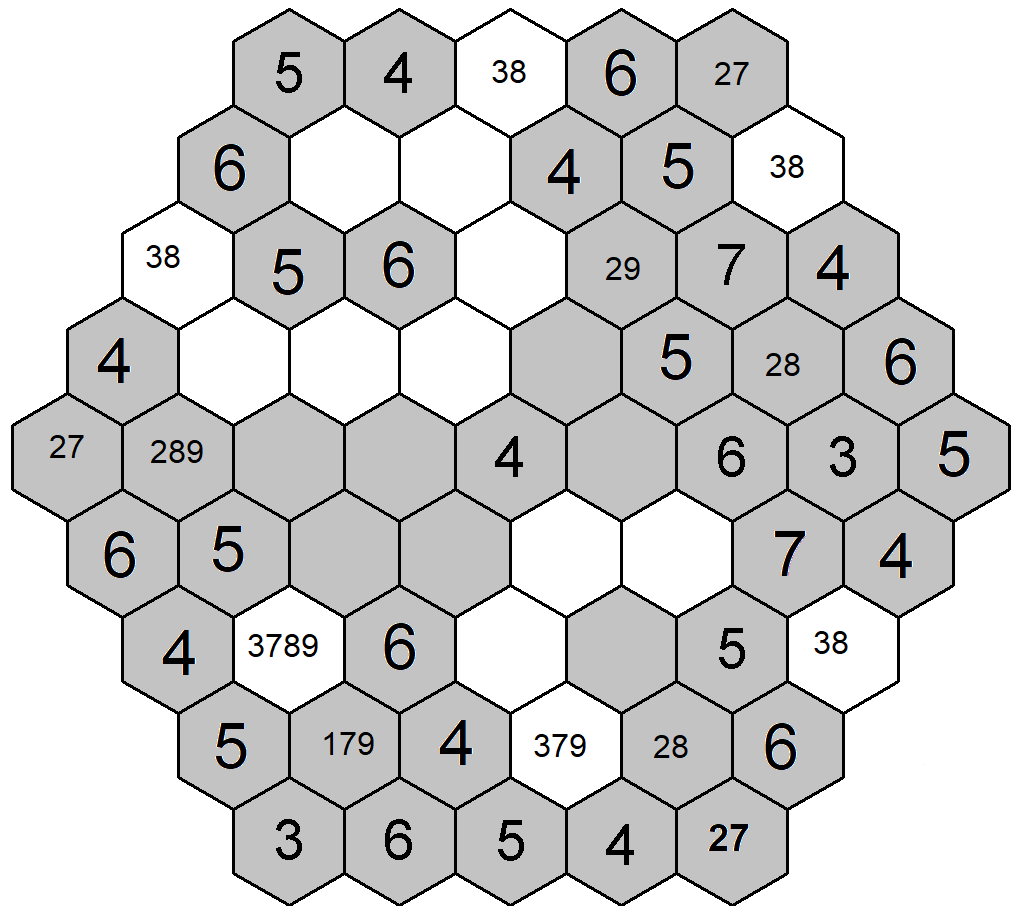
Ufff, abych se neuvpiskoval, zkusím kombinovat. Podívám se, kolik trojek a sedmiček musím napsat do celého obrazce. Číslo 3 se bude vyskytovat minimálně sedmkrát, protože mimo pěti směrů na levých diagonálách, kde být musí, ho už mám vepsáno na dalších dvou diagnálách. Číslo 7 se bude vyskytovat nejméně šestkrát.
Teď pozor. Pátá pozice na prvním řádku je průsečík dvou pětipolíčkových směrů. Pokud bych umístil číslo 2, v obou směrech musím doplnit číslo 3. Tím by se číslo 3 vyskytovalo na všech levých diagonálách, tedy by bylo v obrazci celkem 9x. Pokud se ale podívám na pravé diagonály, 9x tam číslo 3 vepsat nelze, nemohl bych tedy stvořit 9 sousledných skupin polí na pravých diagonálách. Na prvním řádku páté pozici tedy bude číslo 7.
Díky doplněné sedmičce na prvním řádku mohu dále doplnit sedmičku na čtvrtý řádek, kde mi zbylo poslední volné pole na druhé pozici. Následně doplním sedmičku na druhý řádek třetí pozici. Poslední úkon spojený s číslem 7 je umazání sedmičky ze vpisku na osmém řádku. Doplnění sedmiček mi pomohlo v mém druhém zobrazení zaměřené na trojky a mohu doplnit trojku na první pozici třetí levé diagonály, která je poslední možností pro číslo 3 v této skupině polí.
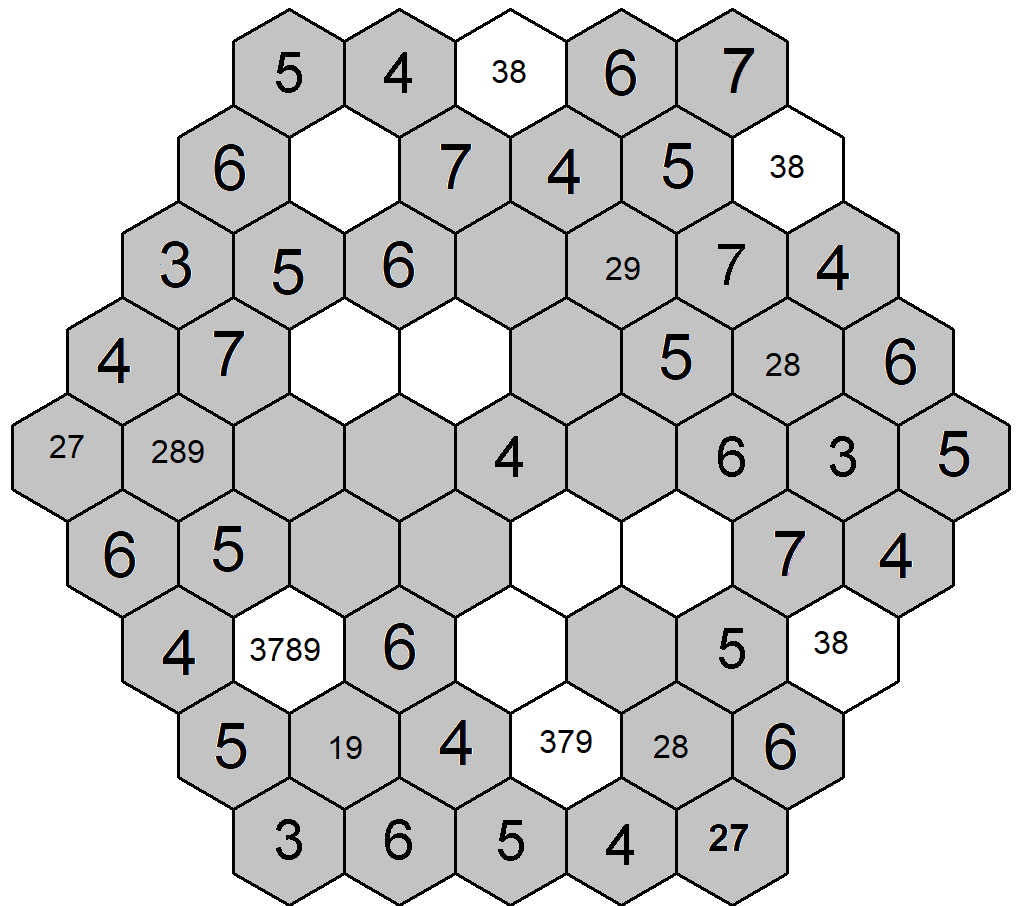
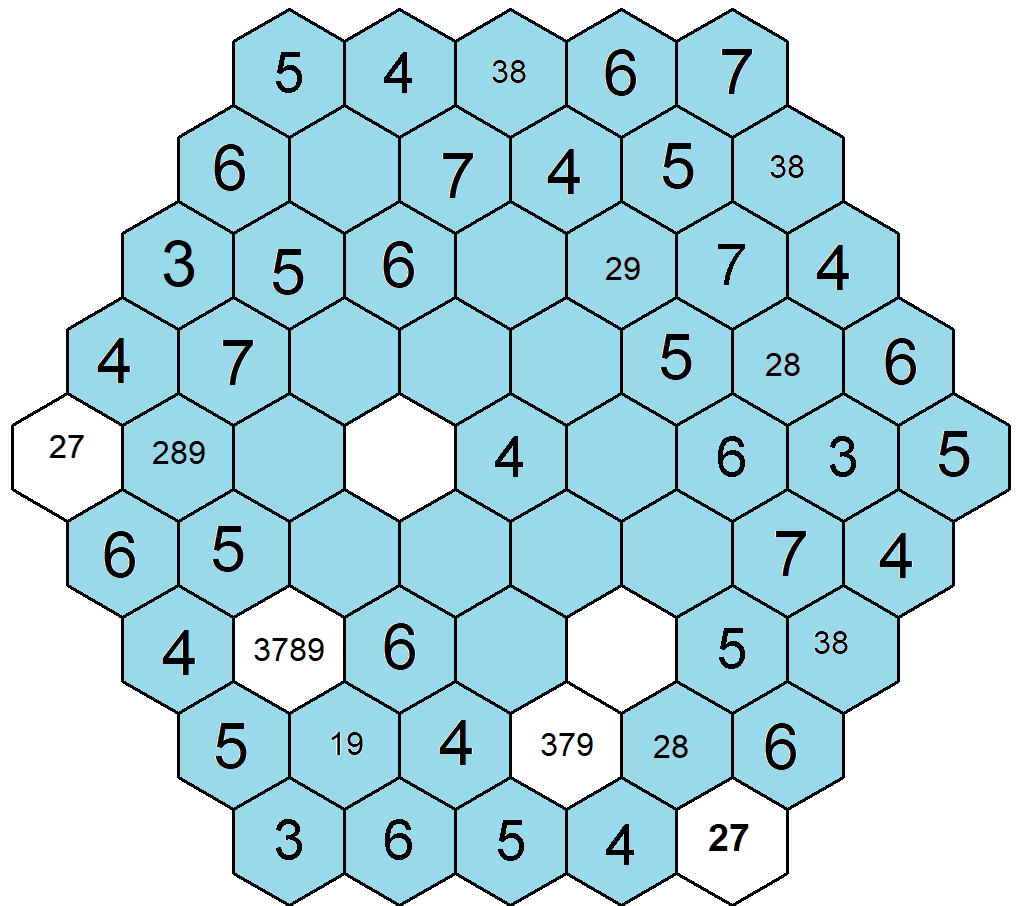
Na osmém řádku na druhé pozici mám vpisek 19 a dvě křižující se šestipolíčkové skupiny polí – osmý řádek a druhá levá diagonála. Využiji vpisků 19, abych si v obou směrech omezil výskyt dalších čísel. V obou směrem nám vzniknou skupiny 1-6 nebo 4-9.
Na druhý řádek druhou pozici bychom mohli dopsat vpisky 2389, nicméně druhá pravá diagonála nám tyto vpisky omezí na 39, v případě doplnění čísel 28 by nám na druhé pravé diagonále chyběla trojka. Na třetí řádek čtvrtou pozici můžeme dopsat vpisky 18, přičemž čísla 29 jsem z tohoto pole vyloučil, protože by ve skupině polí chybělo číslo 8.
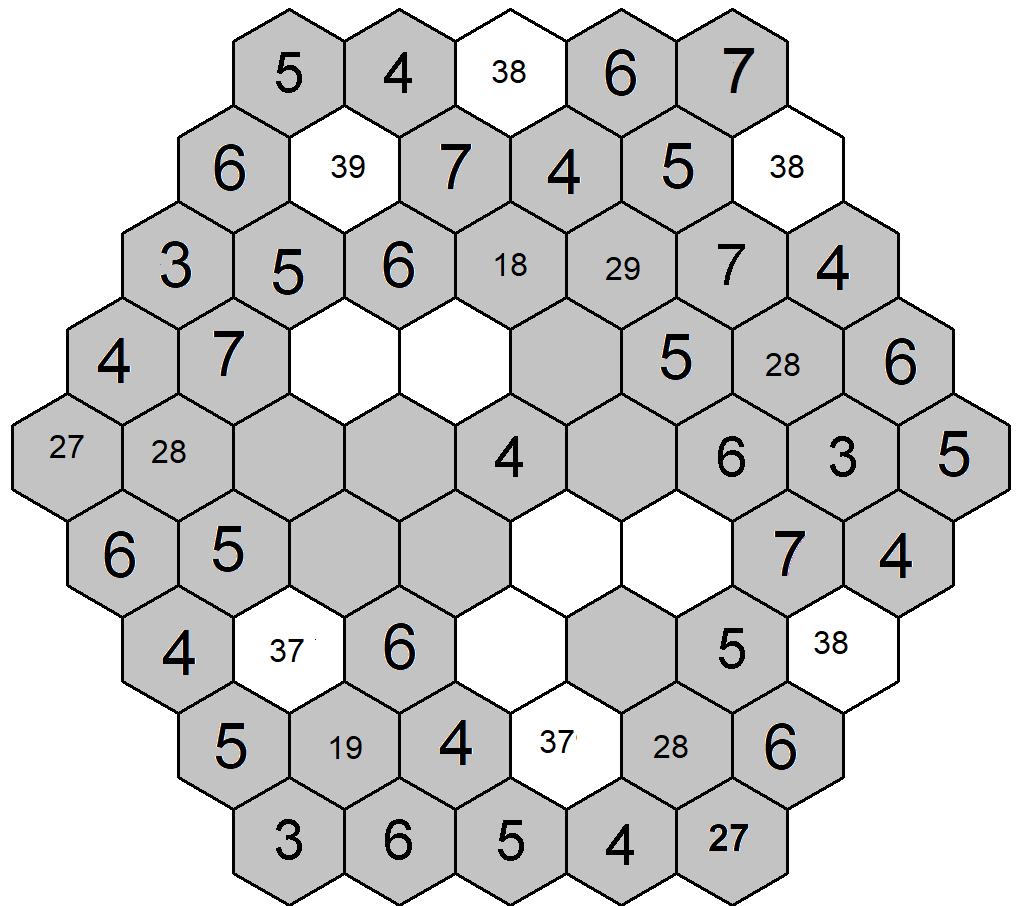
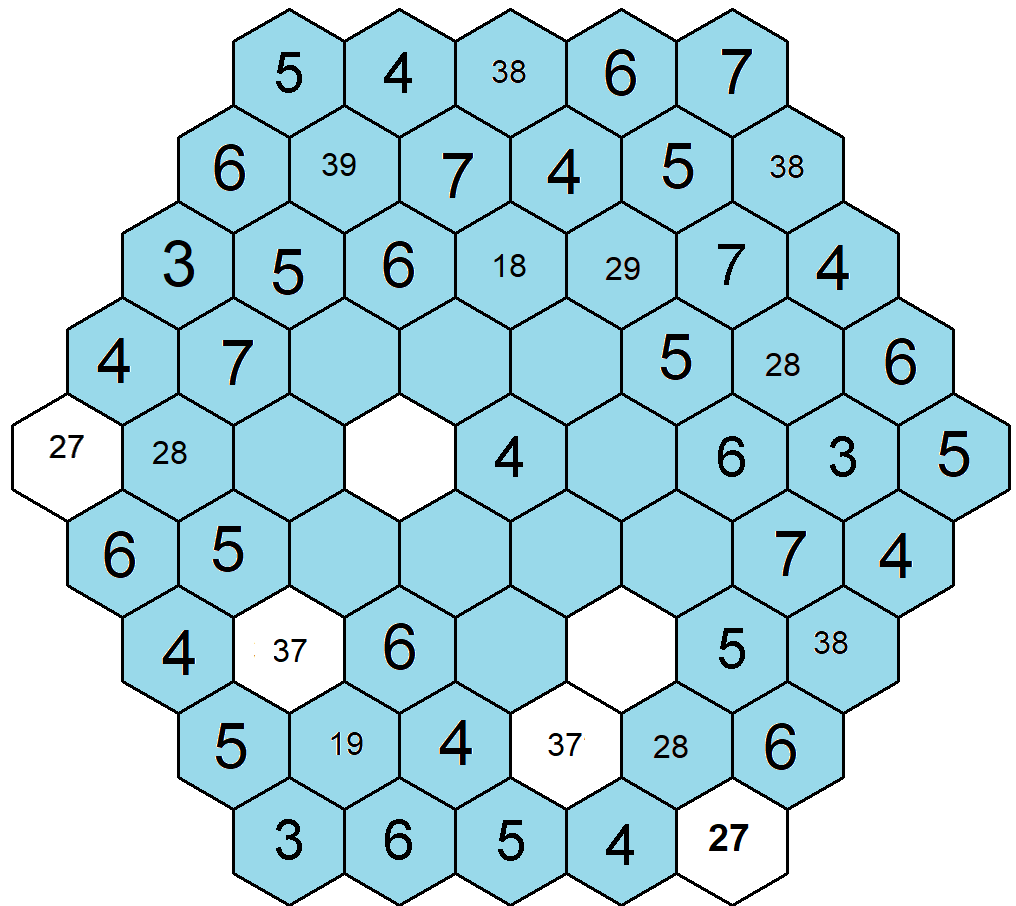
Vypadá to, že jen přes vpisky to nedocvaknu, vrátím se tedy zpět k lince, kterou jsem si vytyčil na začátku a v které se snažím upínat během celého řešení úlohy. Nyní je pro mě důležité určit rozmístění čísel 3 a 7. Na osmém řádku druhé pozici mám již zmiňované vpisky 19. Pokud zde doplním číslo 1, vzniknou mi na šestipolíčkových skupinách řady 1-6, pokud doplním číslo 9, vzniknou mi dvě řady 4-9. V obouch případech se mi objeví na bílých polích čísla 3 nebo 7. V levém obrazci vidím, že pokud bych doplnil číslo 1, tím pádem na druhé pozici sedmého řádku a čtvrté pozici osmého řádku bude číslo 3, pak mi ale tyto trojky vyblokují obě poslední možnosti doplnění čísla 3 na řádku čtvrtém. Tento krok tedy učinit nemohu a na osmém řádku druhé pozici musí být číslo 9. Doplním si obě řady 4-9 a díky doplnění dvou sedmiček v těchto řadách následně určím umístění zbylých sedmiček v obrazci, konkrétně je doplním na první pozici pátého řádku a pátou pozici devátého řádku. Doplnění sedmiček mi pomůže k doplnění trojek, které mohu postupně doplnit na čtvrtou pravou diagonálu, pak na šestý řádek a nakonec čtvrtou levou diagonálu. Doplním další čísla na první, druhý a sedmý řádek.
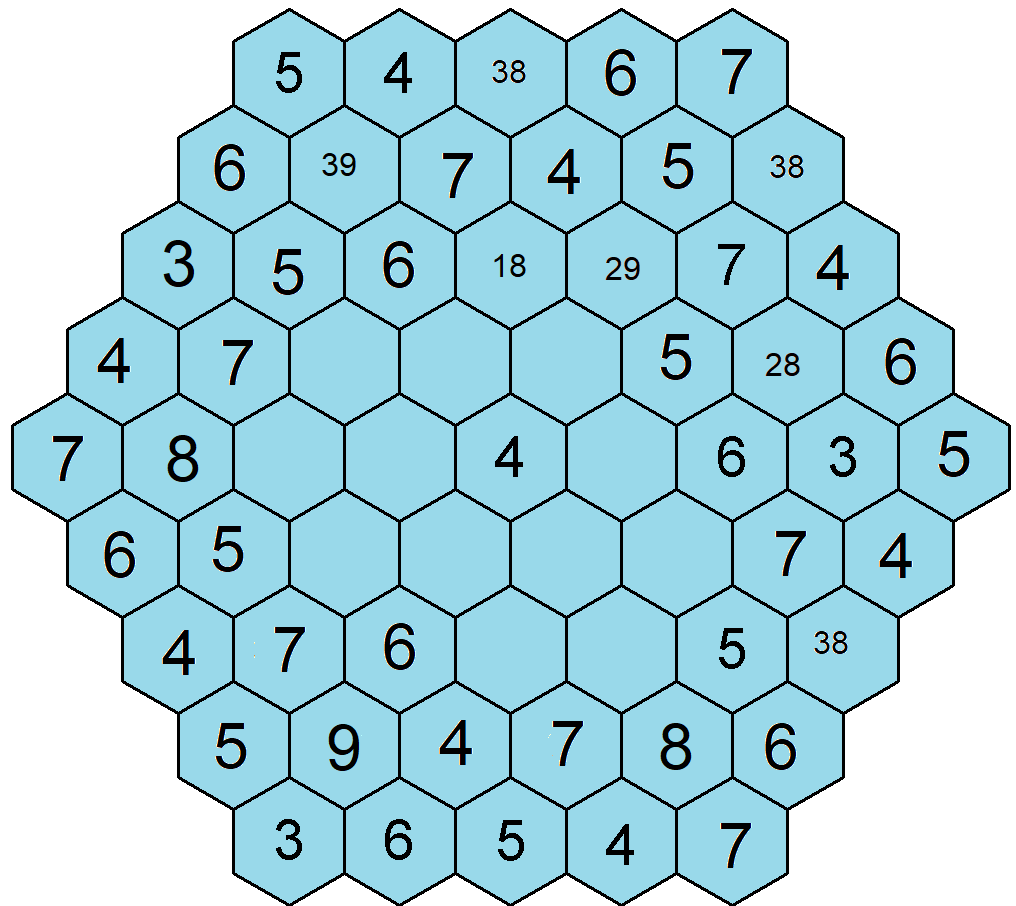
Jsme téměř u konce, schizofrenní rozdělení už nechám být a doplňuji poslední čísla do vytvořených řad. Na sedmý řádek přijde číslo 2, na pátou levou diagonálu číslo 1, na sedmou pravou diagonálu číslo 8, na šestou pravou diagonálu číslo 2, na šestou levou diagonálu číslo 8 na třetí pozici a tak dále… než dosáhneme vytouženého konce.
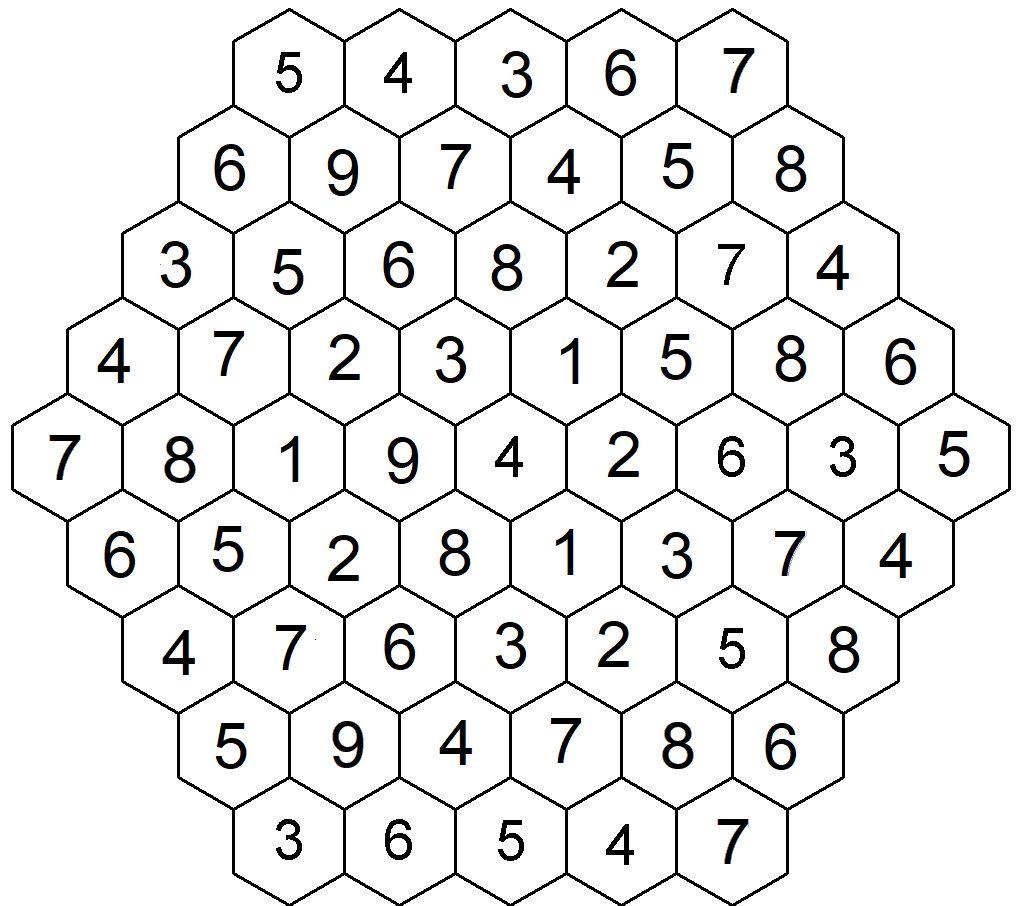
sepsal Pavel Kadlečík
Další návody na řešení úloh:
Antidiagonální zabijáček
Tipy na úlohy z českého kola Sudoku GP 2020
Zabijáček
Sudoku klony
Theme by Danetsoft and Danang Probo Sayekti inspired by Maksimer
