Dozvuky autorské soutěže: Návod na Čtveráky

Sepsal jsem návod na Čtverácké renbanové klony od Kuby Hrazdiry, která zvítězila v 2. kole autorské soutěže v sekci sudoku a následně se objevila v 568. kole DS. Důvody k sepsání návodu jsou dva. Prvním je počet odeslaných řešení v DS, kdy číslo úspěšných řešitelů výrazně kleslo oproti předešlým týdnům DS. Zdá se, že si někteří z pravidelných luštitelů DS naběhli a úlohu nezdolali. Druhý důvod je, že pocity z luštění hrály hlavní roli při vítězství úlohy v autorské soutěži, jinak řečeno pro to, co při luštění hodnotitelé zažili a co museli vymyslet, jí dali na první flek. Pro nás pořadatele autorské soutěže je to nové poznání, loňská sudoková úloha Čísla na diagonále zvítězila v autorské soutěži díky jinému charakteru - pro jednoduchost nápadu a příjemné luštitelné provedení. Úlohy podobné Čtveráckým renbanovým klonům jsou v DS vítané, abychom přiměli luštitele se vydat a ukázat vše, co v nich je.

Zadání úlohy

• podle bodu d) pravidel si ozelením diagonálu,
• podle bodu c) pravidel si ozelením všechna pole prvního, pátého a devátého čtverce 3x3, jelikož políčka symetrická od vyznačené diagonály leží v jednom čtverci 3x3 a nemůžou být stejné hodnoty (podle pravidel klasického sudoku),
• podle bodu c) pravidel si ozelením dvě zadaná čísla - 3 a 9, která jsou si symetrická podle vyznačené diagonály a zároveň obsahují různá čísla,
• podle bodu b) mi zešednou nejen vlasy, ale též tři políčka symetrická podle vyznačené diagonály od tří šedě zadaných políček,
• podle bodu b) si doplním do šedého pole na 1. řádku ve 4. sloupci číslo 6,
• podle bodu a) platí, že všech 6 nynějších šedých políček (3 zadané + 3 zešedlé) obsahují číslo, které se rovná velikosti renbanu, v němž se nacházejí,
• k tajuplnému bodu e) se kriticky vyjádřím na konci návodu. 

Jak dál? První myšlenka při začátku luštění sudoku se mi vždy stočí ke klasickému sudoku. Zde nemohu nic vyjma pár vpisků. Lze si dopsat možnosti do šedých polí, předpokládám, že čísla budu postupně vyřazovat, až se mi nakonec vyloupne číslo velikosti renbanu. 

Ha, vidíte co já? Renban s 6, který má být veliký 6 polí, se nemůže dotýkat stranou jiných zadaných šedých polí. A zbývá mi na vykreslení renbanu právě jen 6 políček, tak si je tam namastím. A též si zazelením políčka sousedící stranou s mým šestkovým rebanem.

Jaká čísla může obsahovat šestkový renban? Vypíšu všechny 4 možnosti:

123456

234567

345678

456789

Šestkový renban bude určo obsahovat čísla 456, které jsou součástí všech možností, dále tři čísla ze zbylých 123789. Zároveň si při jakékoliv luštění renban sudoku připomínám, že jakmile si určím další číslo, vyselektujeme mi moje úvaha nejméně jedno číslo, které nebude součástí renbanu. Např. kdybych určil číslo 7 za součást renbanu, hned vím, že číslo 1 nebude jeho součástí a takhle si postupně hraju s renbany.

Dopíšu si vpisky 45 do všech možných políček renbanu, odeberu vpisky 45 z šedého "řídícího" políčka dalšího renbanu, který se nachází ve stejním čtverci 3x3 (mluvím o políčku na 3. řádku v 6. sloupci a políčku na 6. řádku ve 3. sloupci).

Zaměřím se na druhý z renbanů ve druhém, resp. čtvrtém čtverci 3x3. Jé, já jsem slepej, v políčku na 3. řádku v 6. sloupci nemůže být číslo 3 ani 7, které ho atakují. Takže mi zbývá pouze 2 a 8. Pojďme se zamyslet, co se stane, když umístím číslo 2. Potřebuji dojkový renban s číslem 2. Mám možnosti 12 nebo 23. Pak kouknu na 7. řádek 3. sloupec. Políčko musí být součástí renbanu, ale nemůže díky již zadaným číslům obsahovat 1 ani 3 a tím se mi sen o dvojkovém renbanu celý zbortil. Renban bude osmičkový! A vyznačím si alespoň jedno další šedé políčko renbanu.

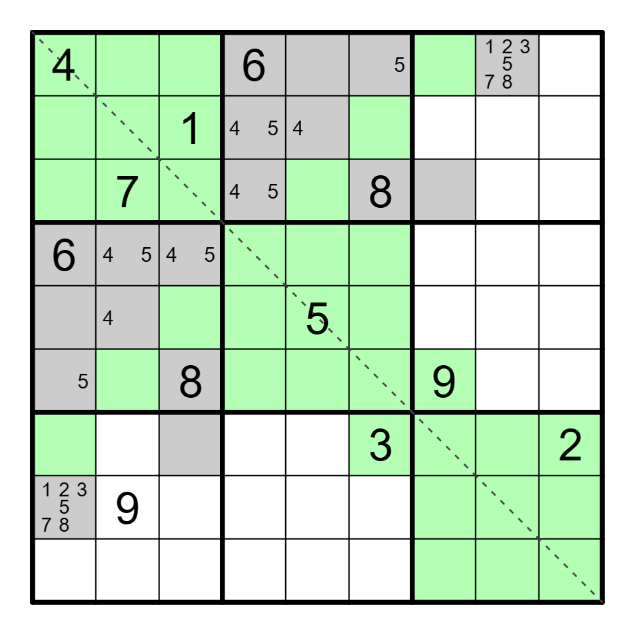
Než skočím jako hladový pes po nově odhaleném osmičkovém renbanu, vrátím se k situaci ve 2., resp. 4. čtverci 3x3, kde mám šestkový renban. Jeho součástí nebude číslo 8, zbývají mi dvě možné kombinace čísel - 123456 nebo 234567. Jeho součástí tedy nebude ani číslo 9 a poslední zelené pole zabere číslo 1 nebo 7. Do čtvrtého čtverce 3x3 doplním 9 na jediné volné zelené pole (5ř3s), na čež krásně nesymetricky doplním 9 do druhého čtverce 3x3 (2ř6s). Ve čtvrtém čtverci 3x3 nemohu doplnit na poslední zelené pole číslo 7, bude obsahovat 1 a tím se mi zfinalizuje obsazení šestkového renbanu na čísla 234567. Číslo 1 doplním na zbylá zelená pole 2. a 4. čtverce 3x3. Šedá políčka šestkového renbanu ...mě už to unavuje, co vás? Přejmenovávám renban na švestkáč.  Švestkáče zaplavím vpisky od 2 po 7. Zároveň mi číslo 7 vypluje pouze na 1. řádku (resp. 1. sloupci), pak mohu číslo 7 umazat ze vpisků dalšího renbanu na 1. řádku (resp. v 1. sloupci).

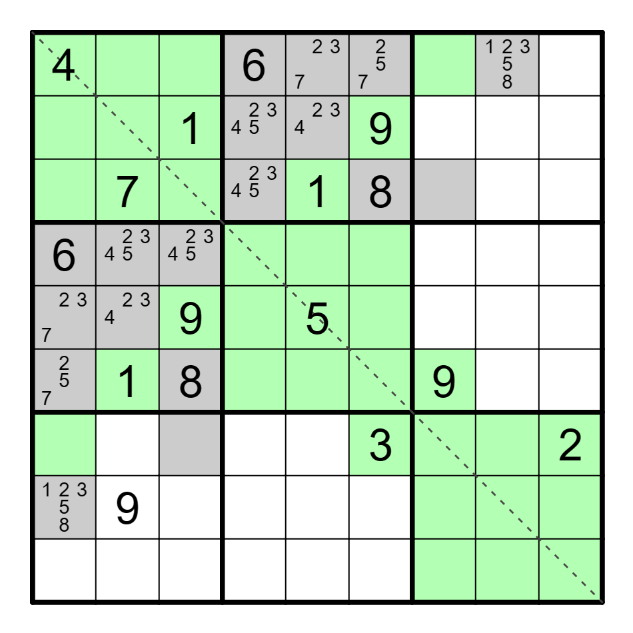
Že bych si mohl zahrát i sudoku? Lup 9 do 1. čtverce 3x3 a hnedka do 3. čtverce 3x3. Uff, už jsem si  potřeboval zahrát sudoku. Doplnil jsem devítky do 3. a 7. čtverce, které jsou si symetrické podle vyznačené diagonály, ale obě 9 leží nesymetricky. Z čehož mi plyne, že jejich políčka ozelením. A hned zároveň mohu ozeleněná políčka vyznačit symetricky podle diagonály, jelikož jakékoli zelené pole má svého symetrického zeleného kamaráda. A co se nestalo? Uzavřel jsem zelenou barvou malinký jedničkový renban, šedé pole bylo označeno již v zadání, obsahuje tedy číslo rovnající se velikosti renbanu - 1.

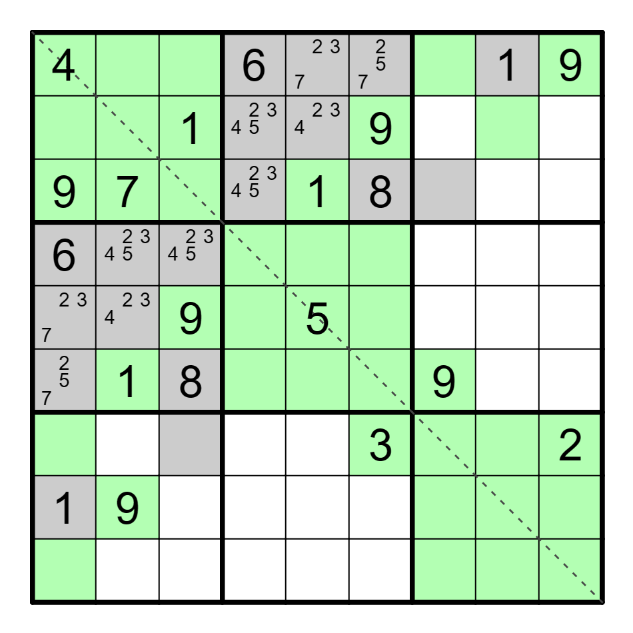
Kudy se vydat dál? Buď se budu věnovat osmičkovému renbanu, v tuto chvíli si dokonce zahrávám s myšlenkou, zda se nám nevejde na bílá pole ještě jeden renban? Těžko říci, pravidlům úlohy by to neodporovalo. Též se mohu věnovat číslům na zelených polí, pár jsem jich doplnil, nesymetricky, mohou trochu rozjet tabulku. Vracím se zpátky k pravidlům úlohy, jestli mě něco nenapsadne. Bod a) jsem využil, čísla 6, 1 a 8 mi určují velikost renbanů. Bod b) jsem pro jedničkový a švestkáč též využil, nevím, jak bude vypadat osmánek.  O bodu c) jsem před chvílí psal, tuším, že pravidlo bude potřeba používat až do konce luštění tabulky. Bod d) je už dávno off-topic. Když jsem úlohu luštil prvně, právě v této fázi a opětovném přečtení bodu e) jsem si začal zpívat Ovčáci, čtveráci, vy jste naši vičku, i tu čočovičku, vypásli. Že by byl Kuba sedlák a skryl tam něco z písně? Tomu se u nás říká nápověda jak stehno.  

Zaměřuji se na osmánka vpravo nahoře. Pole 3. a 6. čtverce 3x3 již obsahují čísla 9, součástí osmánka tedy nebude 9, nemohu ho nikam na bílé pole umístit, osmánkovi tudíž budou patřit čísla 12345678, z čehož číslo 8 jsem již umístil. Jednička je v tabulce již 5x, pomůže mi eliminovat, kam ji do osmánka nacpu. Vychází mi pouze na dvě pole 4. řádku (resp. 4. sloupce). Následně sudokově doplním 1 do 5. čtverce.

V bílém sektoru 7. a 8. čtverce 3x3 mi pak pomůže číslo 3 v levém spodním osmánkovi. Abych mohl do osmánka umístit 3, našel jsem pro něj pouze 3 políčka v 7. čtverci 3x3 (resp. 3. čtverci 3x3), napíšu si vpisky pro číslo 3. 

Vypadá to, že jsem s osmánkem moc nepohnul, ale při pohledu do 1. sloupce a na první tři řádky vidím jeden luxusní trik, snad ho dokážu popsat srozumitelně.  Koukněte do 1. sloupce, kam mohu umístit číslo 3? Osmánek mi vyblokoval umístění 3 níže (na 7. a 9. řádku), zbývá pouze 2. a 5. řádek. Na prvních třech řádcích bude v tabulce 3x číslo 3, to dá rozum už z pravidel klasického sudoku. Poprvé bude 3 v 1. čtverci 3x3, podruhé ve švestkáči a potřetí v horní části osmánka (ve 3. čtverci 3x3). S renbany na prvních třech řádcích musím mít na paměti, že zároveň umísťují 3 do symetrických polí v prvních třech sloupcích. Takže mám 3 řádky (resp. 3 sloupce) na umístění tří trojek. Když umístím 3 na 2. řádek do 1. sloupce, tak já nezaberu pouze jeden řádek, ale vlastně též jeden sloupec, ale ne symetricky identický sloupec, takže v reálu zabírám dva řádky a dva sloupce (tj. zabírám pozice v renbanech na 2. řádku a v 1. sloupci, kam jsem 3 právě umístil, též zabírám symetricky promítnuté pozice v renbanech na 1. řádku a v 2. sloupci). A to by znamenalo, že mi ve výsledku na umístění všech trojek do renbanů na prvních třech řádcích (resp. v prvních třech sloupcích) nezbude místo. Aby mi zbylo místo, musel bych v 1. čtverci 3x3 umístit 3 pouze na pole 1ř1s, 2ř2s nebo 3ř3s. Při umístění 3 do všech ostatních polí 1. čtverce 3x3 mi místo nezbude.

Co z mé úvahy plyne? V 1. čtverci 3x3 bude 3 pouze na polích  2ř2s nebo 3ř3s (třetí potecionální pole 1ř1s mám již obsazené 4), na téže pole si mohu do dvojpisku doplnit sudokově čísla 6. Do zbylých polí 1. čtverce 3x3 si napíšu vpisky 258. Druhým velkým krokem na základě popsané úvahy je šup s 3 na 5. řádek 1. sloupce, symetricky pak do 5. sloupce na 1. řádek.

Nyní mohu doplnit do švestkáče 7. Dále si doplním si vpisky na 1. řádek a do 1. sloupce.

Přemýšlím, které další číslo v tabulce mi může pomoci ve svlečení osmánka do naha? Vidím 2 na zeleném poli v 9. čtverci a zároveň musí být někde na osmánkovi. Zadaná dvojka mi eliminuje 7. a 9. řádek (resp. 7. a 9. sloupec), zbývá 8. řádek pro sloupce 3-6 (resp. 8. sloupec s řádky 3-6). Vidím další trik, trochu podobný našemu předchozímu. Když dám 2 do osmánka ve 3. čtverci 3x3 (resp. 7. čtverci 3x3), vznikne mi potřeba z pravidel sudoku umístit číslo 2 na 1. řádek tabulky a do 1. sloupce tabulky a jediné místo pro dvě čísla je 1. čtverec 3x3, kde se nemůže vyskytnout více než jednou. Takže to nejde. Dvojka bude v osmánku na 8. řádku ve sloupcích 4-6 (resp. v 8. sloupci na řádcích 4-6). Nevím, jestli mi to pomůže, ale mám radost za špičkovou logickou úvahu.  Ale pomůže. Obdobnou úvahu provedu s číslem 5. Když bych chtěl dát 5 na osmánka v 3. čtverci 3x3 (resp. v 7. čtverci 3x3), dostanu se do podobné tísně s umístěním 5 na 1. řádek a do 1. sloupce. Osmánek bude mít tudíž 5 v 6. čtverci 3x3 (resp. 8. čtverci 3x3). Již zadaná 5 vprostřed sudoku spolu se vpisky 5 ve štvestkáči mi vyloupnou jediná dvě místa pro 5 na osmánkovi. Rýsuje se nám osmánek a bude pěkně nataženej.  Změnil jsem barvu vpisek, která značí čísla na osmánkovi, na šedou, ať je to názornější, kam až se může natáhnout, přičemž nezapomínejme, že má pouze 8 políček.

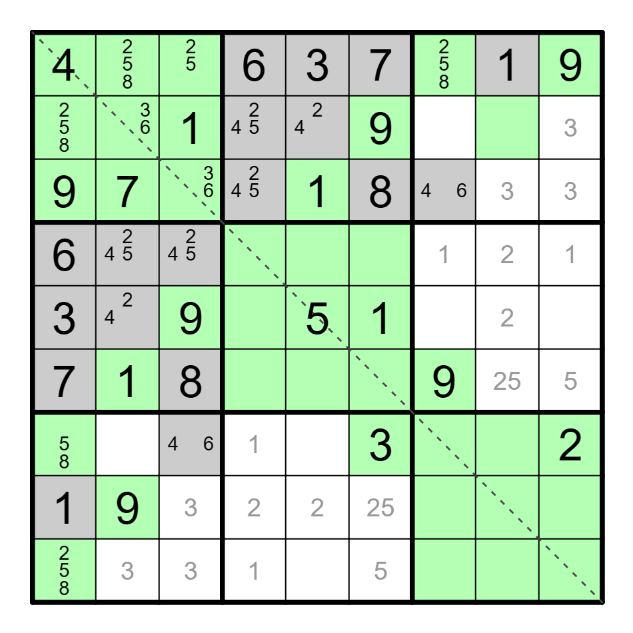
Ještě mi vrtají hlavou čísla 258, nemohl jsem s nimi vykouzlit něco více? Hoďte voko na poslední tři sloupce a číslo 2. V 9. sloupci dvojku již mám, v 8. sloupci tři varianty pro umístění dvojky na osmánkovi, na 7. sloupec mi zbývá 1. či 2. řádek. Bryskně kouknu na celý 3. řádek a už mi zbývá pouze jedna možná pozice pro dvojku, na švestkáčovi, která mi ho následně celý rozkryje. Úvaha mě zalila radostí, pokračuji sudokově v 5. čtverci 3x3 doplněním dvojpisku 26, z čehož se mi v 6. čtverci 3x3 ukáže jediné místo pro 2 na osmánkovi!

Není to úplně můj styl, ale zkusím úlohu kompletně zaplevelit vpiskama. Já se v nich někdy ztrácím, ale takhle věřím, že najdeme nějaké hezké dvojičky či trojičky. Jak jsem začal, vylezlo mi hned číslo 3 a 4 v 5. čtverci. Vpisků přibývá, takže se zabrzdím na plevelení pouze 5., 6. a 8. čtverce 3x3.

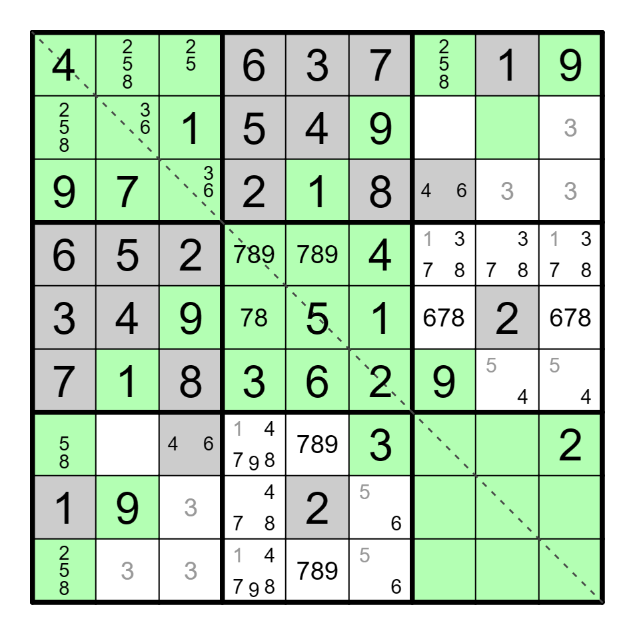
Myslím, že se blížíme k odhalení polí osmánka. Popíšu úvahu, která mě jako první trkla do očí po ovpiskování. Jedná se o 5. sloupec a 8. řádek. Dole v 5. sloupci vidím čísla 789, vím, že 8 a 9 nemůže být součástí osmánka, 8 už je určena, 9 jsme vyřadili. Když by se tato čísla nacházela v 5. sloupci na 7. a 9. řádku, pak osmánek bude protažen na 8. řádku od 4. do 6. sloupce. Do 6. sloupce musím, čeká tam na mě osmánková 5, do 4. sloupce taky musím, abych se propojil se zbytkem osmánka. Takže pole na 8. řádku ve 4. sloupci je šedé, kterému symetricky odpovídá pole na 4. řádku v 8. sloupci. Korelací vpisků v obou polích (47 vs. 378) mi vypadne jediná možná 7. No jo, ale umístit 7 do obou polí následně způsobí, že ji nemám kam dát v 5. čtverci 3x3.

Zdá se vám má úvaha moc složitá? Je, strašně, omlouvám se, takové mě napadají furt, vůbec nevím, proč to popisuje tak složite.  Zkusím jinak. Osmánek dole má dvě odělené části, políčko s 8 ve 4. čtverci 3x3 a políčko s 2 v 8. čtverci 3x3 a já je musím spojit. Čtvrtý sloupec dole na 7. až 9. řádku je propojovací plocha, symetricky je jí část osmánka vpravo na konci 4. řádku. Jak označím šedé pole v 8. čtverci 3x3, hned označím šedě jemu symetrické ve 6. čtverci 3x3. Číslo na takovém poli se musí následně nacházet v 5. čtverci v části, která je obsazena čísly 1256. To jsou jediná možná čísla k propojení osmánka. Čísla 256 již ve 4. sloupci a na 4. řádku mám, jedinou zbývající možností k propojení je číslo 1. Tedy číslo 1 bude na šedém poli, ostatní pole 4. sloupce dole budou zelená, stejně tak konce 4. řádku. K propojení 1 s číslem 2 budu potřebovat ještě jedno pole, z vpisek v uvedených polích je možná jako část osmánka pouze 7. Pro větší přehlednost si eliminuji vpisky, ozelením si pole na 8. řádku ve 4. sloupci, kde 1 být nemůže (obdobně políčko na 4. řádku v 8. sloupci). Jako bonus doluštím kompletně 5. čtverec 3x3.

Teď jsem si vzal do hlavy, že chci vykreslit celého osmánka. Situaci popíšu na spodním osmánkovi. V 8. čtverci 3x3 vím, že budou přesně 4 šedá pole (zaplněná čísly 1275) patřit osmánkovi. Ve 4. čtverci 3x3 je jedno šedé pole s 8, na 7. čtverec 3x3 mi zbývají 3 šedá pole, která vyplním čísly 346. Jedno pole už šedé mám, hledám zbylá dvě. Ve 3. sloupci na 3. řádku mám dvojpisek 36, který mi omezuje, že by všechna tři šedá pole byla ve 3. sloupci. Jedno z šedých polí s čísly 3 nebo 6 bude ve 2. sloupci, druhé číslo z této dvojice, plus číslo 4 bude ve 3. sloupci. Kdybych se pokusil umístit šedé pole na 9. řádek do 2. nebo 3. sloupce, budu následně potřebovat k propojení s číslem 2 v 8. čtverci 3x3 dvě cestičky políček, jedna by vedla po 7. řádku, druhá by vedla po 9. řádku a tolik šedých políček použít nemohu. Šedá políčka tedy budou na 7. řádku ve 2. a 3. sloupci a na 8. řádku ve 3. sloupci. Nakreslím si i druhého osmánka, dosadím čísla a už letím tabulkou k cíli!

 

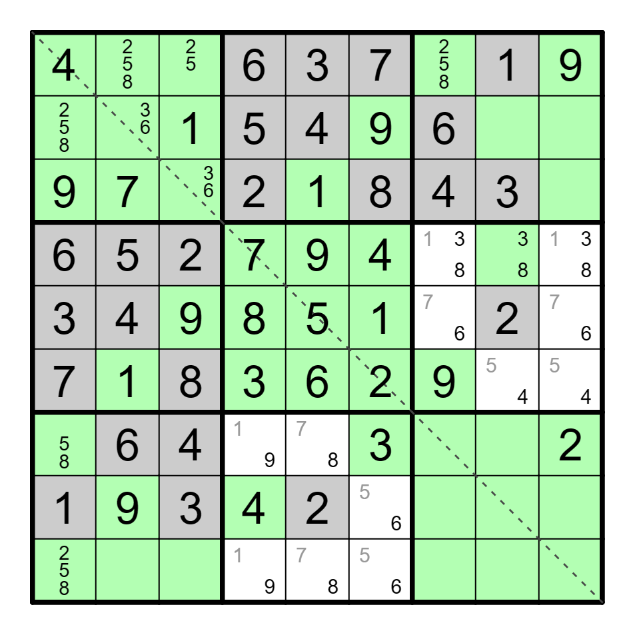
Za mě nářez. Tuším, že Čtveráci jsou příkladem úlohy, kterou luštíme každý trochu jinak. Při psaní návodu jsem ji luštil podruhé a stoprocentně jsem ji prvně zčásti rozlousknul jiným způsobem, jen si už nepamatuji jak.  Našli jste jiný způsob? Můžete napsat do komentářů, rádi se pokocháme.

 

A co nám vlastně říkala nápověda v názvu úlohy? Kuba vysvětluje zde.

 

Držím palce, ať vám jde luštění podobných kousků od ruky! Ovčáci, čtveráci, vy jste... 

 

sepsal Pavel Kadlečík