Čtvrté sudokové kolo WPF GP 2021 si zahrálo 36 českých luštitelek a luštitelů, ve spolkových číslech to vychází na 24 "halasáků" včetně dvou milých slovenských členů. Oficiální výsledky kola byly stvrzeny docela se zpožděním, my jako v předešlých kolech přidáváme rady na řešení vybraných úloh a věříme, že vám pomohou v dalších bitvách.
Následující sudokové kolo GP (od 7. do 10. května 2021) je zařazeno mezi turnaje HALAS ligy 2021. Holandští autoři nabízejí tréninkové úlohy na webu národní asociace https://www.wcpn.nl, vřele doporučujeme si jimi zahřát mozky na provozní kapacity před samotnou soutěží. ![]()
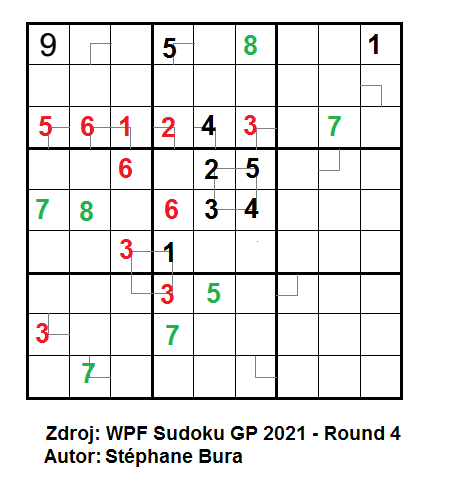
4. kolo WPF Sudoku GP 2021 – od 9. 4. do 12. 4. 2021
Úlohy si autorsky podělili tři francouzští mušketýři - Édouard Lebeau, Erwan Bernard a Stéphane Bura, roli d'Artagnana se ujal György Herke z Maďarska. V soutěžní sadě se nacházelo plných 7 klasik, 5 známějších variant, 2 kousky představovaly kombinace více variant a poslední úlohou byla nová varianta nazvaná Remote Clones. Francouzsko-maďarský autorský tým si úlohy kola rozdělil zhruba polovinou.
Při hledání informací o francouzských autorech jsem narazil na youtubový kanál SudoKanard („sudokový kačer“), kde Éda natáčí videa, jak luštit vybrané logické úlohy z online soutěží. Řešení úloh čtvrtého kola GP je namluveno v angličtině, jinak většina videí z jiných soutěží je určena přátelům sudoku, kteří vládnou francouzštinou.
Pro doplnění uvádím, že György se účastnil českých mistrovství v sudoku či logice v předešlých letech, takže ho někteří účastnící českých soutěží znají. Při jeho návštěvě Prahy v roce 2017 si mě najal šošon za průvodce po pamětihodnostech a musím říci, že s Györgym (a Yuheiem Kusuiem) to byl příjemný a pohodový den.
Prvním kouskem, který si vezmu do zubů, je sedmá klasika. Nebudu ji luštit celou, ukážu pouze jednu situaci. Začněme s doplnění hrstky čísel, které budu pro ukázku potřebovat. Ve 4. čtverci mohu dát číslo 2 pouze na 4. řádek do 1. sloupce. V 9. čtverci mohu doplnit číslo 7 pouze na 9. řádek do 7. sloupce. Do 7. čtverce mohu doplnit číslo 4 na 8. řádek do 3. sloupce. Pokud jsem líný na vpisky, tak jsem tak nějak skončil, což je škoda.
Ve 2. sloupci mi do 4. čtverce zasahují čísla 7 a 9 a po doplnění čísla 2 v předešlých krocích mi zbývají pouze dvě pole na doplnění čísel 7 a 9. Na 4. až 6. řádku 2. sloupce mi tak vznikne trojička vpisků 456 a pro 1. a 9. řádek 2. sloupce mi zbývají čísla 13.
Kouknu do 4. sloupce a tam je krásná čtveřice. Čísla 5, 6, 7, 3 mi ve 4. sloupci vbíhají do 5. čtverce a mám pro ně prostor akorát. Ve 4. sloupci na 4. až 6. řádku mi zbyde trojička vpisek 489 a obdobně jako v 2. sloupci si mohu napsat dvojičku vpisek pro 1. a 9. řádek 4. sloupce, konkrétně čísla 12.
Tak a teď technika, u které zapomínám na její název, ale sami vidíte, že ve 2. a 4. sloupci mám napsánu dvojičku čísel 12 v prvním případě a 13 v druhém. Toho mi plyne, že číslo 1 bude na 1. řádku ve 2. sloupci a na 9. řádku 4. sloupce, nebo bude číslo 1 ve 2. sloupci na 9. řádku a na 1. řádku ve 4. sloupci. Výsledkem je, že mohu číslo 1 vyloučit ze všech dalších sloupců 1. a 9. řádku.
A proč jsem toto všechno dělal? Kouknu do 3. čtverce. Číslo 1 mohu ve 3. čtverci doplnit pouze na 2. řádek do 8. sloupce a na 3. řádek do 7. sloupce. Číslo 7 díky doplněné 7 v úvodní části mohu doplnit pouze na 2. či 3. řádek 9. sloupce. Pro doplnění možností čísla 3 si pomohu v 1. čtverci, kde může být pouze na 1. řádku v 1. nebo ve 2. sloupci a následně pouze v 8. či 9. sloupci 2. řádku. Obdobně si napíšu vpisky pro čísla 4 a 5 ve 3. čtverci. A teď kouknu na 1. řádek do 8. sloupce, čistokrevný „singl“ a je jím číslo 2.
Pokud bych si kouzlo s 1. a 9. řádkem 2. a 4. sloupce neuvědomil, měl bych při pečlivém vpiskování dospět do situace, že mi na 1. řádku ve 4. sloupci a v 8. sloupci vyvstane dvojička vpisků 12, která vede k zapsání čísla 3 do 2. sloupce na 1. řádek.
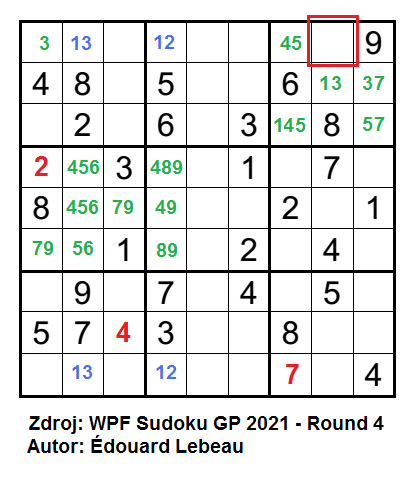
U Symmetric Unequal platí, že pole, která jsou protilehlé kolem středu tabulky (tj. kolem pole na 5. řádku v 5. sloupci), nemohou obsahovat stejná čísla. Úlohu řeším podobně jako klasické sudoku, ale dávám po očku pozor na pole, která jsou „symetricky spojena“. Kdo si rád píše vpisky, tak si myslím, že uspěje a že mu neuniknou místa, která znamenají posun v tabulce. Já si v příkladu řešení psát vpisky nebudu, ale o to více se musím soustředit na negativní podmínku. Začínám v místech, kde je nejvíce čísel, tím pádem mám největší pravděpodobnost úspěchu.
Ve 4. čtverci sudokově doplním číslo 2 na 4. řádek do 1. sloupce. Další 2 naleznu v 3. čtverci, kde jsou pouze dvě místa na její doplnění a symetricky protilehlá 2 mi eliminuje pozici na 3. řádku v 7. sloupci. Doplněnou 2 využiji pro 6 ve 3. čtverci, zde se může nalézat pouze v 8. sloupci a v 6. čtverci mi zamíří na 5. řádek do 9. sloupce. Následně doplním 6, 2 a 1 do 5. čtverce. Navážu na to doplněním 5, 4 a 3 na 4. řádek. 5. řádek zkompletuji sudokově a doplním postupně 4, 3 a 8. Ve 4. čtverci pro doplnění 1 využiji symetrii.
Stále hraji jako klasiku, dokonce to převažuje, přičemž si kontroluji, kam které číslo dát nemohu kvůli podmínce symetrie. V 6. čtverci mohu doplnit sudokově 8 na 4. řádek do 9. sloupce. Pak mi zde zbývají pro číslo 7 pouze dvě pozice v 8. sloupci. Pokud bych ji doplnil na 6. řádek, další 7 bych musel přidat ve 4. čtverci na 4. řádek do 2. sloupce, což je symetrické kolem středu tabulky s předchozí 7. Tento krok musím vyloučit a 7 v 6. čtverci bude na 4. řádku.
Tohle nám šlo, v rámci rekapitulace vyzdvihnu 2 techniky řešení sudoku využitelné všude možně.
1 - Řezání) Podbarvené extraregiony tvaru písmene F a U, leží ze 7/9 v 1. čtverci, respektive v 9. čtverci. Pokud extraregiony uříznu podle čtverce 3x3, v obou případech jsem odřízl dvě pole extraregionu, které se shodují s čísly ze čtverce 3x3 neležící v rámci extraregionu. Pro 1. čtverec to jsou čísla 3 a 7, pro 9. čtverec čísla 4 a 8.
2) Číslo 4 ze 7. řádku mi atakuje 7. čtverec tak, že ho mohu doplnit pouze na tři volná pole extraregionu písmene H. Z čehož mi plyne, že v 8. čtverci mi zbývá jediné pole na doplnění čísla 4.
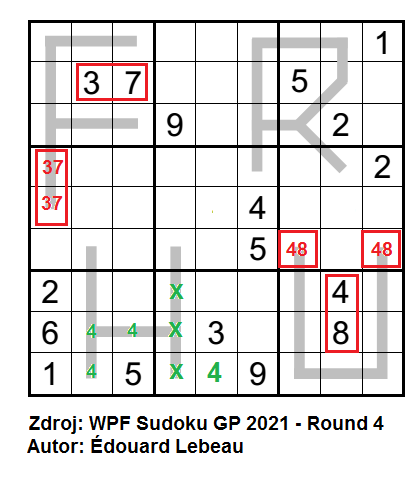
Úloha nabízí více cest k řešení, pokud byste chtěli vidět, jak je řešena autorem, koukněte na video od SudoKanarda. Já se pokusím nabídnout i jiné kroky.
Začínám stejně, na 8. řádku je sousledná trojička, která není tvořena čísly 4 a 7. Bude to 1-2-3, číslo 2 si doplním do 5. sloupce, dvojičku vpisků 13 do 4. a 6. sloupce. Kouknu na obdobnou trojici na 2. řádku. Zde by se nabízelo též 1-2-3 nebo trojice složená z čísel 6 až 9. První možnost nemohu, jelikož v 5. sloupci již 2 mám, trojice bude tedy 6-7-8 nebo 7-8-9, z čehož vím, že obsahuje čísla 7 a 8 a neobsahuje čísla 1 až 3.
Zaujaly mě též vyznačené sousledné páry. V 3. čtverci je sousledná dvojice, která musí obsahovat jedno sudé a jedno liché číslo, ze sudých čísel mohu doplnit pouze 2 na 2. řádek do 9. sloupce a dvojičku vpisků 13 pod něj. Souslední pár v 1. čtverci bude obsahovat číslo 8, což mi vychází sudokově díky 8 na 3. řádku, 8 na 2. řádku v trojičce a 8 v 3. sloupci. Druhým číslem v dvojici bude 7 nebo 9. Sousledný pár v 7. čtverci nebude ze sudých čísel obsahovat 4 a 8, které jsou zadány. Ale ani číslo 2, které mám na 3. řádku ve 3. sloupci a ve 4. čtverci se musí vyhnout vyznačené sousledné trojici, v 7. čtverci následně číslo 2 umístím na 9. řádek do 2. sloupce. Sousledná dvojice 7. čtverce obsahuje číslo 6 a k němu 5 nebo 7. K odhalení sousledné dvojice v 9. čtverci využiji, že z lichých čísel nemůže obsahovat zadanou 5 a 7, dále ani 1 kvůli právě doplněné 2 na 9. řádek, což je jediný sousledný kamarád 1. Pokud bych se podíval pozorně na 8. řádek, snad bych odhalil, že v 8. sloupci nemohou být čísla 1 až 7, tím pádem tu zbývá možnost 89, čímž do sousledného páru nemohu doplnit ani 9. Sousledný pár na 9. řádku bude obsahovat číslo 3 s číslem 4.
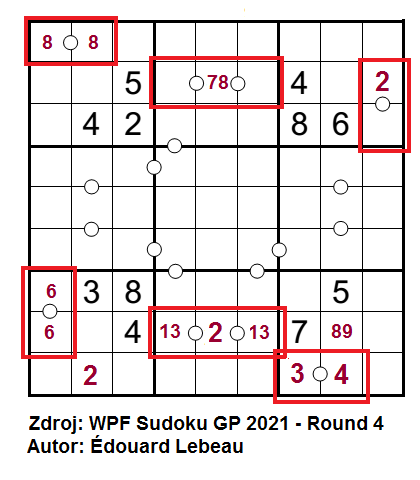
Věřím, že poctivá mravenčí práce každého dovede k cíli, aniž by musel zkoušet divoké kombinace, které luštitele občas pod časovým presem napadají. ![]()
Úloha Frame sudoku má ve své nejobvyklejší podobě zadána všech 36 součtů prvních třech čísel. V Györgyho úloze figurují pouze součty 20 a 21 a budeme ji řešit trochu jinak. Nezbytná je znalost zmíněných součtů, pokud ji váš procesor nepředkládá automaticky, vypsal bych si je všechny vedle tabulky, abych s nimi mohl pracovat. Součet 20 vytvořím z čísel 9-8-3, 9-7-4, 9-6-5 nebo 8-7-5, součet 21 z čísel 9-8-4, 9-7-5 nebo 8-7-6.
V 1. čtverci se mi křižují dvě 20, přičemž nemohu využít zadaná čísla 5 a 6. Pole na 3. řádku v 3. sloupci, kde se oba součty protínají, bude obsahovat číslo 9, do dvacíti dopočítám s čísly 3-8 a 4-7. Zbývající dvě pole patří dvojičce 12. Ve 3. čtverci se mi protínají součty 20 a 21 opět číslem 9, přičemž ani v jednom součtu nemohu využít číslo 7. Součet 21 dopočítám s čísly 4-8 a na součet 20 mi zbývá kombinace 5-6. V 9. čtverci se mi protínají dva součty 21, přičemž nemohu využít čísla 4. Kombinace 6-7-8 a 5-7-9 mají společné číslo 7. Součet 21 na 7. řádku nemůže být 5-7-9, jelikož čísla 5 a 9 jsem určil součtu 20 v 8. sloupci a na 7. řádek do 8. sloupce bych v této možnosti neměl co umístit. Součet 5-7-9 bude v 7. sloupci, 6-7-8 na 7. řádku. Přesunu se do 7. čtverce, kde se mi protínají součty 20 a 21. V součtu 20 na 8. řádku nemohu využít číslo 3 (jež je zadané v 7. čtverci), číslo 4 (zadané na 8. řádku) ani kombinaci 5-7-9, jelikož dvojička 59 bude na 8 řádku v 7. sloupci. Součet 20 tak tvoří čísla 5-7-8. Součet 21 ve 2. sloupci nebude 6-7-8 kvůli zadané 6 ve 2. sloupci, nebude ani 5-7-9, protože dvě čísla z této kombinace využiji v právě odhaleném součtu 20 na 8. řádku a mně se zde součty protínají jen v jednom čísle. Součet 21 ve 2. sloupci bude 4-8-9.
Pro další postup navrhuji doplnit sudokově pár čísel a zaměřit se na součty 20 a 21 na 4. a 6. řádku a ve 4. a 6. sloupci.
Jednou z efektivních technik luštění sudoku, u kterých řešíme paritu čísel, je zabarvování. Když jsem prvně viděl na českých soutěží, jak si luštitelé hrají s pastelkami, říkal jsem si, omalovánky už přeci nejsou pro mě? ![]() Teď na to nedám dopustit. Pokud to přímo úloha svou obtížností nevyžaduje, může se to zdát jako ztráta času, přesto výhodou podbarvení je získání přehledu o celé tabulce a o paritě všech polí, která by se jinak mohla přehlédnout.
Teď na to nedám dopustit. Pokud to přímo úloha svou obtížností nevyžaduje, může se to zdát jako ztráta času, přesto výhodou podbarvení je získání přehledu o celé tabulce a o paritě všech polí, která by se jinak mohla přehlédnout.
V příkladu značím sudé čísla růžově, lichá čísla zeleně. Začnu zabarvením zadaných čísel. Pokračuji u šipky s číslem 1, kde již jedno sudé číslo je, prázdné pole na 9. řádku musí být tudíž liché. Nápověda u šipky s číslem 0 mi pak říká, že všech 6 čísel ve směru šipky je lichých. Poslední, čeho jsem si v úvodní zabarvovaní fázi všiml, jsou dvě pole na 2. řádku. V 6. a 8. sloupci mám již doplněno číslo 8 a na 2. řádku čísla 2, 4 a 6. Pole v 6. a 8. sloupci na 2. řádku tím pádem budou lichá.
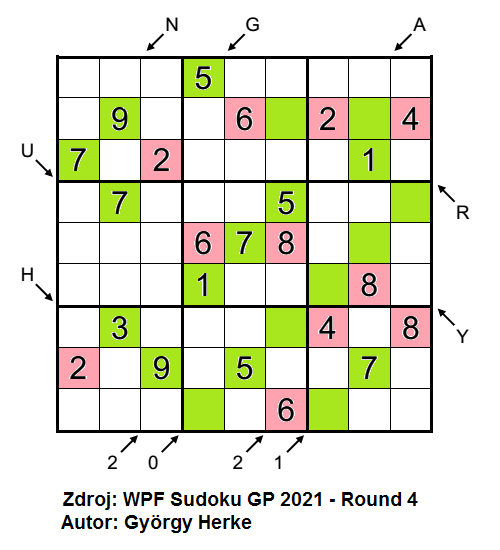
Teď se zaměřím na zakódované nápovědy u šipek. Nezmínil jsem celkovou koncepci úlohy, HUNGARY 2021, moc pěkné. Všimnu si, že některá písmena představují velmi nízká čísla, protože směřují pouze na 2 až 3 pole, dále si pomohu informací o paritě polí, pro které jsem ji již odhalil. Písmeno H může představovat 0 až 3 sudá čísla, písmeno U 0 až 5 sudých čísel, písmeno N 0 až 2 sudá čísla, písmeno G 0 až 3 sudá čísla, písmeno A 0 až 7 sudých čísel, písmeno R 0 až 2 sudá čísla, písmeno Y 0 až 4 sudá čísla. Do rozmezí od 0 do 3 mi pasují 4 různá písmena (H, N, G a R), z čehož vím, že 0, 1, 2 a 3 sudá čísla ve směru šipky nemohou představovat zbylá písmena U, A a Y. Písmeno Y bude značit 4 sudá čísla, písmeno U 5 a pro písmeno A připadá 6 či 7 sudých čísel. Hned si obarvím sudou barvou pole ve směru písmen U a Y a pečlivě koukám na zbytek tabulky, co se mi z toho vyloupne. Počet 2 sudých čísel pro šipku pod 5. sloupcem mám rázem splněn, zazelením si zbývající dvě pole.
Nyní se snažím odhalit paritu co nejvíce polí. Přitom mohu využít technik klasického sudoku, jelikož zakreslení parit mi zmenšilo můj manévrovací prostor, kam čísla doplnit. Zářným příkladem je číslo 7 na 6. řádku, které mohu umístit pouze na zelené pole v 7. sloupci, z čehož následně umístím 7 do 9. sloupce na 1. řádek. Na 3. řádku v 6. sloupci mám označeno sudé pole, čísla 2, 6, 8 zde již využít nemohu, bude zde 4. Když kouknu na celý 6. sloupec, tak mi zbývá ze sudých čísel doplnit číslo 2, které nemůže být na 8. řádku, políčko zabarvím do zelena. Posledním příkladem, jak pokračovat dále, je 9. čtverec, kam mi směřuje číslo 6 z 9. řádku a nemohu ho umístit na zelená pole, napíšu ho na 8. řádek do 9. sloupce. Zbývající pole 8. řádku budou též sudá, zbývající pole 9. sloupce budou lichá a tak dále….
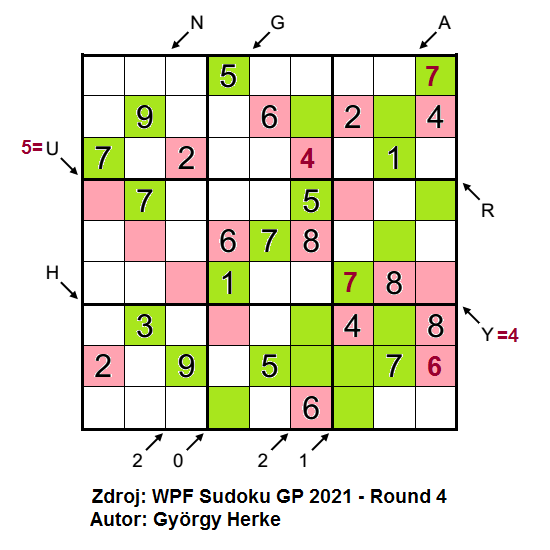
Techniku zabarvování lze využít u všech úloh, kde víme informaci o paritě polí. V sudém či lichém sudoku (kde je pouze u vybraných polí řečeno, zda jsou sudá/lichá), u variant oblíbených autory GP jako je Mathrax sudoku nebo Battenburg sudoku, v některých případech dokonce u sousledného sudoku, kde vím, že každá značka souslednosti mi spojuje 1 sudé a 1 liché číslo.
Malé značky mezi políčky značí buď číslo větší, nebo rozdíl čísel. Rozmístění malých čísel opět graficky symbolizuje rok 2021.
Začnu tím, že si označím, co malá čísla představují. Malé číslo 1 nemůže být nikdy tím větším ve dvojici, takže všechny značky 1, a že jich v tabulce je, budou značit rozdíl dvou čísel. V 5. sloupci si všimnu, že první tři značky 2 odspodu též nemohou být číslem větším kvůli zadané 1 v 5. sloupci na 8. řádku. Ale nejvíce mne zaujal 9. sloupec. Na 6. až 9. řádku je sousledná čtveřice a výše jsou tři pole, mezi nimiž je dvakrát číslo 6. Ha, pojďme to rozmotat! Dvě 6 mezi políčky můžou znamenat dvě varianty. Buď bude 6 v obou případech větším číslem, nebo bude jednou číslem větším a jednou rozdílem. Třetí možnost (= dvakrát rozdíl o 6 u čísel 1 až 9) prostě nejde. Přemýšlím o první možnosti. Pokud by byla 6 dvakrát větším číslem, znamenalo by to dvě čísla menší než 6 ve zbývajících polích. Ale co ta čtveřice sousledných čísel? Musel bych najít 6 čísel menších než 6, takže zavrhuji. Pro tři políčka s dvěma malými 6 bude platit, že na kraji trojice bude číslo 6, uprostřed číslo z rozsahu 1 až 3 a na druhém kraji čísla 7 až 9. A opět přemýšlím nad souslednou čtveřicí. Může být tvořena kombinací 1-2-3-4 nebo 2-3-4-5, v obou případech v ní budou čísla 2, 3 a 4. Což mi rozlouskne horní trojičku 6-1-7, jednička bude na tuty uprostřed. Dolní souslednou čtveřici tvoří sekvence 2-3-4-5 a zbývající pole 9. sloupce obsadí vpisky 89.
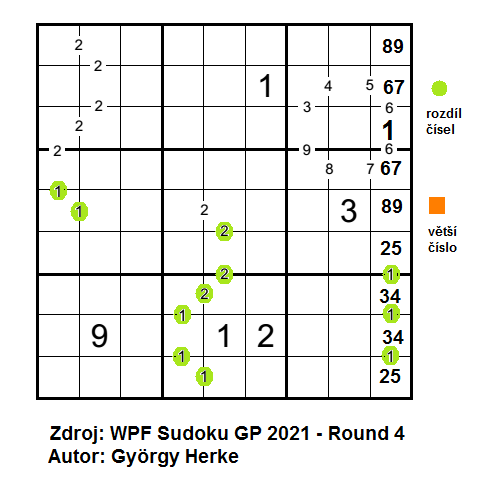
Pokračuji rozmotáním vztahů ve 3. a 6. čtverci. Začnu od malého čísla 5 na 2. řádku. Vztah nebude určovat větší číslo, jelikož mám v pravém poli již vpisku 67. Tudíž číslo 5 je rovno rozdílu, což mi dává možnosti pro levé pole 1 nebo 2. Číslo 1 již ve 3. čtverci je, rozdíl 5 tak činí čísla 2 a 7. Následně přijde na 4. řádek 9. sloupce číslo 6. Malé číslo 7 vpravo od čísla 6 na 4. řádku mi říká, že neznačí rozdíl (mohl bych použít pouze čísla 1-8 nebo 2-9), ale to, že v levém poli od 6 bude větší číslo 7. Obdobně malá 8 mi značí větší číslo na 4. řádku v 7. sloupci a malá 9 mi značí větší číslo mezi 3. a 4. řádkem 7. sloupce. Na 2. řádek do sedmého sloupce bude pasovat číslo 6 jako rozdíl 3 od devíti a rozdíl 4 od dvou. Nyní mohu doplnit čísla 8 a 9 do 9. sloupce a 3. čtverec zaplnit číslem 3 a vpisky 45.
Přesunu se do 1. čtverce a bádám nad tím, co mi říkají malá čísla 2. Zopakujme, pokud by měla 2 značit větší číslo z dvojice políček, pak by druhým číslem byla 1. Ale ta nejde v 1. čtverci umístit do vztahu na 3. řádku, ani v 2. sloupci mezi 3. a 2. řádek. Do pole na 2. řádku v 2. sloupci nemohu umístit čísla 1 ani 2, tudíž pro vztah mezi 1. a 2. řádkem 2. sloupce platí taktéž, že malé číslo 2 představuje rozdíl. Položím si spekulativní otázku, mohou všechna malá čísla 2 v 1. čtverci představovat rozdíl? Tomu by odpovídala pouze sekvence 1-3-5-7-9, kterou umístit nemohu. Poslední neznámý vztah 2 na 1. řádku tak bude představovat větší číslo.
Úloha je pěkná tuhoňka. Sekvence 4 čísel s rozdíly 2 mezi sousedními poli může být pouze 1-3-5-7 nebo 2-4-6-8, oboje myšleno shora dolů. Správnou variantu mi rozsekne pole na 4. řádku v 1. sloupci, kde bych v případě druhé možnosti nemohl umístit číslo 6. Platit bude tedy varianta druhá, v tomto poli bude vpiska 59. Sekvence tří sousledných čísel ve 4. čtverci bude 5-6-7 nebo 9-8-7.
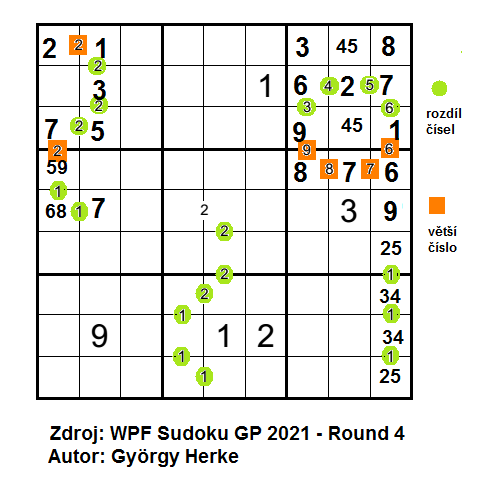
Vzkaz autora hráčům byl „vybojujte si to až do konce“, takže poslouchám a jdeme se podívat na vztahy mezi čísly v 5. a 8. čtverci. Vztah 2 na 5. řádku by v případě rozdílu musí být složen ze sudých čísel 2-4 nebo 4-6, v případě, že označuje číslo 2 za větší, tak by zde byla nám známá kombinace 1 a 2 a v poli na 5. řádku v 5. sloupci by byla 2, tedy taktéž sudé číslo. Označím si proto všechna sudá čísla v sekvenci. Pokud se podívám do 8. čtverce, rozmístění sudých čísel (a následně i lichých) lze provést pouze dvěma způsoby. Pokud beru za první číslo sekvence 9. řádek a 5. sloupec, pak směrem vzhůru ji tvoří čísla 9-8-7-6-4-6-8 nebo 3-4-5-6-8-6-4. Na 5. řádek 5. sloupce vychází v prvním případě číslo 8, v druhém případě číslo 4. S číslem 8 bych se dostal do sporu, v 1. sloupci 5. řádku mám totiž vpisku 68. Do samého srdce tabulky umístím číslo 4. Kdo úlohu v rámci soutěže zdolal, má můj obdiv. ![]()
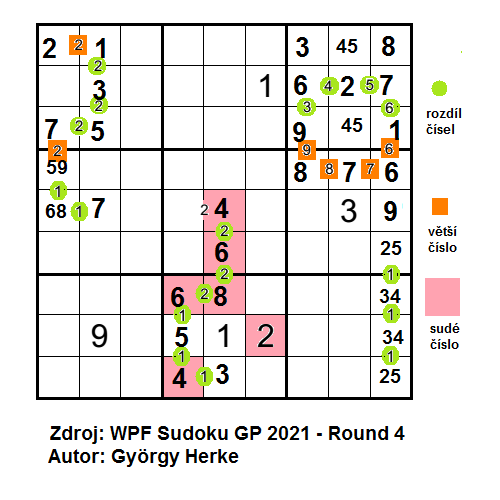
Varianta sudoku, kterou vymyslel a pro GP připravil Stéphane Bura. Už od pohledu pracná k vyřešení. Od začátku vpiskuji a ono to, světe div se, jde. Úloha mi tímto stylem luštění připomíná vnitřní mrakodrapy či jiné úlohy, v nichž pole se značkou (či šipkou) může obsahovat maximálně číslo dané vzdáleností značky od okraje tabulky.
Pro potřeby návodu jsem si ovpiskoval všechny značky s hodnotou maximálně 5. Do vpisků jsem nezařadil čísla 1 či 2 v případech, pokud značka ukazuje na pole v této vzdálenosti a přitom se pole nachází ve stejném čtverci, viz např. značka na 4. řádku v 6. sloupci nemůže obsahovat čísla 1 nebo 2, jelikož by se obě identická čísla nacházela v 5. čtverci. Dále pracuji se vpiskami. Na 3. řádku v 5. sloupci bude číslo 4, jelikož čísla 1 až 3 využiji v dalších polích řádku. Na 1. řádku 4. sloupce bude číslo 5, jelikož číslo 4 jsem právě doplnil do 2. čtverce a čísla 1 až 3 obsahují další pole 4. sloupce. V 5. čtverci mám tři pole s možnostmi 234, pak značka na 6. řádku ve 4. sloupci bude 1 a značka na 4. řádku v 6. sloupci bude 5. Doplněná 4 v 5. sloupci mi určí číslo 4 na 5. řádek do 6. sloupce. Pokud se podívám pozorně na značky na 4. a 5. řádku 5. sloupce, pak níže položená mi směruje na 3. či 2. řádek v 5. sloupci. Ale nemůže ukazovat na 3. řádek s číslem 4, jelikož bych nemohl jeho „čtyřkový klon“ umístit na 5. řádek. Na 5. řádku bude značka 3, na 4. řádku značka 2.
Umažu si vpisky podle doplněných čísel, kde to jde. Číslo 5 doplněné na značku v 1. řádku, mi ukazuje na políčko klonu v 9. sloupci. Na 3. řádku v 1. a 2. sloupci mohou čísla na značkách být nejvýše 6.
Teď se zaměřím na 3. řádek. V 6. sloupci mám vpisky 13, ale číslo 1 zde být nemůže, protože bych na 3. řádek nedoplnil klon čísla 5, které bude v 1. či 2. sloupci řádku. Doplním tedy 3 a na dalších dvou značkách řádku směrem doleva doplním čísla 1 a 2. Číslo ve 2. sloupci 3. řádku může být jedině 6, jelikož na něj ukazují dvě značky z 3. řádku a použití čísla 5 by neumožnilo doplnění jeho klonu do 3. sloupce, ani do 4. sloupce. Alternativním způsobem, jak rozhodnout o umístění 5 a 6 na 3. řádku je fakt, že kdybychom dali 6 do 1. sloupce (a 5. do 2. sloupce), na 3. řádku by značky ukazovaly na stejné číslo, naopak v 1. a 2. sloupci by obě značky směřovaly do 7. čtverce na dvě různá pole, kde se ale stejné číslo může vyskytnout jen jednou.
Doplním si čísla (případně vpisky) pro pole, kde mají být obsaženy klony. Mohu začít poli, na které ukazuje značka 6 na 3. řádku. V 8. sloupci 3. řádku mohou být pouze čísla 789, pokud se podívám na jeho klon ve 2. sloupci, tak ukazuje na další značku. A sem mohu doplnit pouze číslo 7, s vyššími čísly bych se na 9. řádku dostal mimo tabulku. Na číslo 5 na 3. řádku ukazuje číslo 4, doplním klon 5 do 5 sloupce. Značka 4 na 5. řádku ukazuje na klony, které ve 2. čtverci mohou být pouze čísla 678, podle 4. čtverce ale zbývá jedinou možností 8. Značka 3 v 1. sloupci na 8. řádku ukazuje na klony, kterým nyní může být jen číslo 8. A takto chirurgicky odhaluji jeden klon po druhém.
sepsal Pavel Kadlečík
Theme by Danetsoft and Danang Probo Sayekti inspired by Maksimer