Následuje autorský postup řešení úlohy Sčítanky z 18. kola dlouhodobé soutěže na stránkách HALAS.
Vyplňte tabulku čísly 1 až 9 tak, aby se stejná čísla neopakovala v žádném řádku, sloupci ani ve vyznačených menších čtvercích.
Číslice v každém řádku tvoří, zleva, jedno čtyřciferné, jedno trojciferné a jedno dvouciferné číslo. Jejich součet je zadán vpravo od řádku.
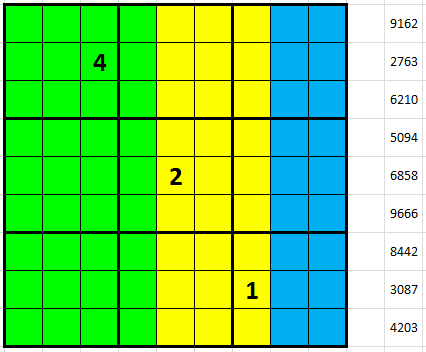
Napřed si pojďme ujasnit, jak je složeno číslo, které je součtem řádku. Budu používat takřka šachovou notaci: označíme řádky shora písmeny A až I a sloupce odleva čísly 1 až 9. Pak má tedy platit, že
součet = 1000*A1 + 100*(A2 + A5) + 10*(A3 + A6 + A8) + 1*(A4 + A7 + A9)
Čísla v řádku jsou pochopitelně navzájem různá. Jdeme-li odzadu, od jednotek, možné součty jsou 6 až 24; o řád výše, do desítek, by se přenášelo 0 až 2 a možné součty na desítkách jsou tedy 6 až 26; v řádu stovek už sčítáme jen dvě čísla, s přenosem nejvýše 2 dostáváme rozsah 3 až 19; nakonec v řádu tisíců bude součtem to, co napíšeme do políčka X1 nebo o 1 více.
Z této poslední premisy můžeme snadno odvodit čísla v prvním sloupci. Nejasnost by mohla být mezi 1. a 6. řádkem a mezi 3. a 5. řádkem, ale okamžitě odpadne, když si připomeneme, že v řádu stovek je minimální součet 3.
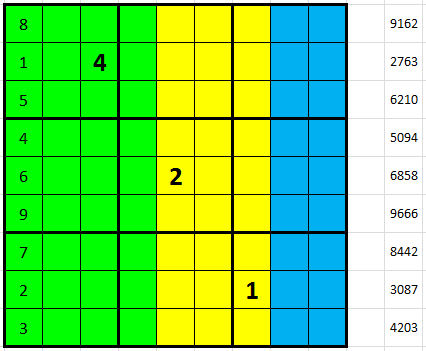
Jak dál?
Když člověk uváží všechna omezení, ukáže se, že složit jednotlivé řádkové součty není vůbec snadné. Až se to může stát jednoznačným. Jak se rozbor řádku dělá? Většinou začnu od jednotek a dívám se, jaké jsou možné součty. (Například v prvním řádku je to A4 + A7 + A9 = 12 nebo 22.) Pro všechny varianty rozvážíme návazné možnosti pro desítky a pak pro stovky. Dopočet k tisícům, které již máme, musí vycházet. Přičemž nesmíme zapomínat na přenosy přes 10. Další omezení mohou vyplývat z toho, jaká čísla se již v tabulce nachází. A potom, součet všech čísel v řádku je 45, tedy součet (A1) + (A2 + A5) + (A3 + A6 + A8) + (A4 + A7 + A9) = 45.
S využitím všech těchto poznatků, lze sestavit následující schéma. Vidíme, že součty jsou ve všech řádcích jednoznačné, s výjimkou 3. a 9. řádku.

Pro ony dva problematické řádky zbývají dvě možnosti, viz následující schémata. A co je důležité, ty dvojice možností jsou provázané; bude-li v řádu stovek nahoře součet 10, dole musí být 11 a naopak. Proč? Zjistíme to ze součtu všech čísel v 2. a 5. sloupci. Ten má být roven 90, pro 7 řádků známe součet jistě a na zbývající dva zůstává 21 dohromady.

Pokročíme o kus dále a pomohou nám k tomu stovky, kde je možností přecijen nejméně. Máme jedno jisté číslo, E2 = 5. Možností v ostatních řádcích zůstává 2 až mnoho, viz levý obrázek. Ale ono je spíš podstatné, jak ty možnosti spolu interagují. Což uvidíme, když budeme na chvíli předpokládat, že I2 + I5 = 10, a to ještě přesněji 1 + 9. V kombinaci s 2. řádkem vyloučíme devítky všude jinde, v 7 řádku zbývá 8 + 5, pak v 8. řádku 6 + 3 a najednou ve 2 sloupci není již žádné místo pro číslo 4, viz pravý obrázek.
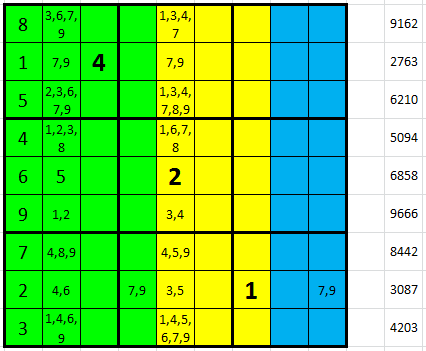
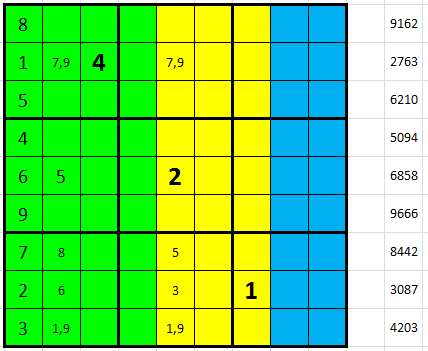
Když odmažeme v posledním řádku ze vpisek variantu 1+9, která tuto neplechu způsobila, posouváme se o krok vpřed. Ve druhém sloupci získáváme dvojičku 4-6 (levý obrázek), po odmazání 4 a 6 ze zbytku sloupce (a odpovídajících variant ve sloupci pátém) se objeví trojička 3-4-5 na polích F5-G5-H5 (pravý obrázek).
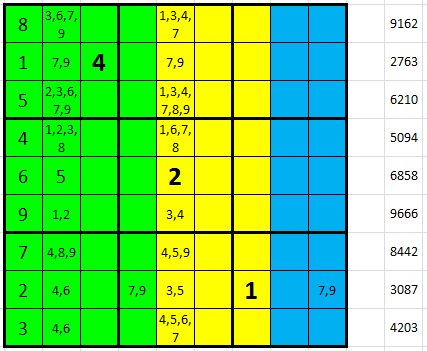
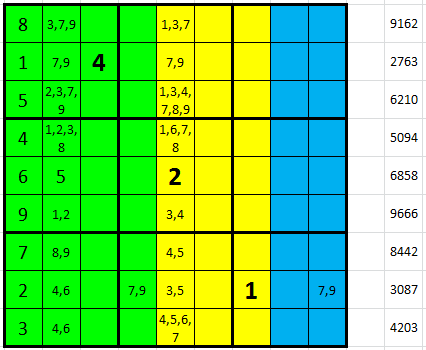
Promazání čísel 3-4-5 z pátého sloupce ponechá v I5 pouze 6-7 což oboje znamená 4 v I2 (levý obrázek). Řetězovou reakcí zůstanou na řádu stovek pouze 4 neujasněná políčka (pravý obrázek).
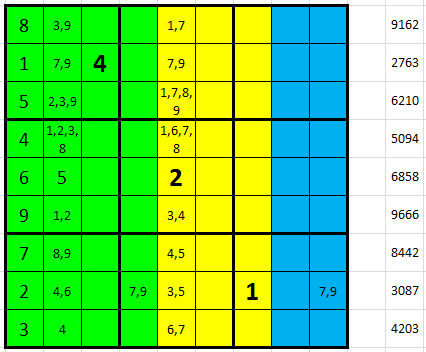
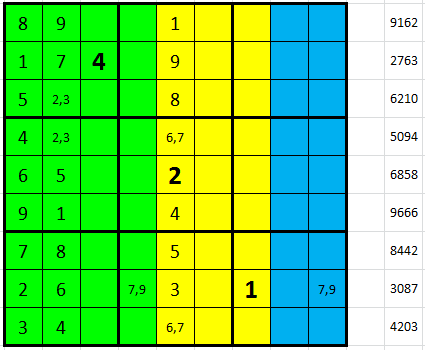
K dalšímu pokroku začneme pracovat také s desítkami. V osmém řádku můžeme rovnou dopsat H3 = 5 a vpisky (levý obrázek). Důležitější úvaha se odehraje v řádku třetím. Připusťme na chvíli variantu, že C2 + C5 = 10 = 2 + 8. Pak C3 + C6 + C8 má být 20. Jenže pro C3 = 3 zbývá 17 a pro C3 = 6 zbývá 14 a ani jednu tuto dvojici již nelze složit (pravý obrázek).
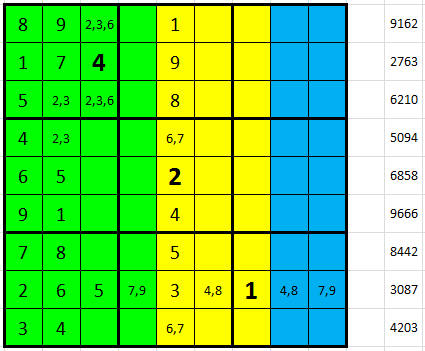
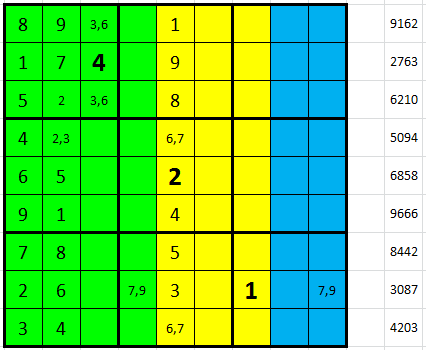
Opačná varianta tedy musí platit, C2 + C5 = 11 a I2 + I5 = 10 (levý obrázek). Zároveň v této variantě máme I3 + I6 + I8 = 19, proto máme v devátém řádku desítky 19 = 2 + 8 + 9 a jednotky 13 = 1 + 5 + 7 (pravý obrázek).

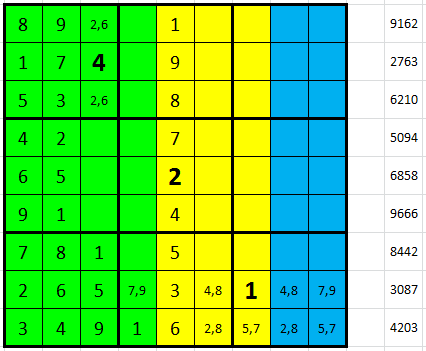
Pokračujeme vpravo dole, H9 = 9 ze vpisek, proto H4 = 7. V sedmém řádku máme desítky 13 = 1 + 9 + 3 v jasném pořadí, a jednotky 12 = 2 + 4 + 6 v nejasném pořadí (levý obrázek). Ve druhém řádku pak můžeme dedukovat desítky 15 = 4 + 5 + 6 a jednotky 13 = 2 + 3 + 8, neboť v políčku B8 nemůže být ze sloupce 3 ani 8 (pravý obrázek).
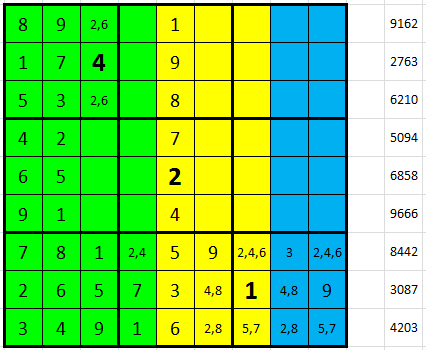
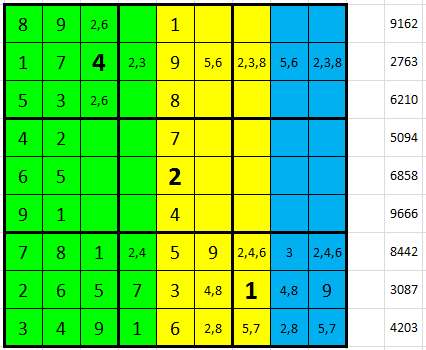
V pátém čtverci máme dvě políčka, kam umístit devítku. Čtvrtý řádek ale není správná volba, protože D4 + D7 + D9 má být 14, bez 9 zůstává 5 a to nesložíme. Máme tedy v pátém řádku jednotky 18 = 9 + 8 + 1 a pak desítky 14 = 7 + 3 + 4, oboje v jasném pořadí (levý obrázek). D6 = 1 doplníme podle klasiky a pak máme ve čtvrtém řádku desítky 18 = 8 + 1 + 9 v jasném pořadí a jednotky 14 = 3 + 5 + 6 v nejasném pořadí (pravý obrázek).
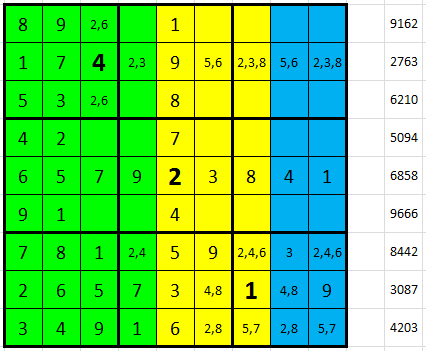
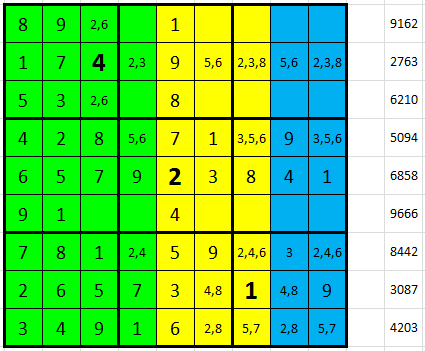
Pokračujeme v šestém řádku, kde máme desítky 15 = 3 + 5 + 7 a jednotky 16 = 8 + 6 + 2. Zbytek tabulky dohráváme klasicky ze vpisek. To už si v podstatě nezaslouží obrázek.
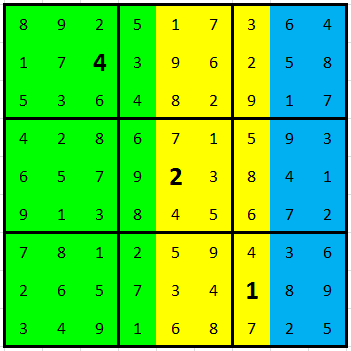
Sepsal 14. 8. 2013 Honza Krtek Novotný.
Theme by Danetsoft and Danang Probo Sayekti inspired by Maksimer