Tapa: Postup řešení

Typ úlohy: Tapa

Zdroj: archiv webu croco-puzzle (úloha z 1. 11. 2013)

Autor postupu a datum: Honza Novotný, 23. 12. 2013

Zadání:

Některá pole v tabulce začerněte tak, aby všechna černá pole souvisela vodorovně nebo svisle a nikde nebyl začerněn celý čtverec 2x2. Pole s čísly při tom není zásadně dovoleno začernit.

Pro pole obsahující čísla platí toto: Když objedeme pole sousedící s tímto polem jednou dokola, získáme sled černých a bílých polí. Čísla udávají délky černých bloků v této sekvenci, přičemž každé číslo patří právě jednomu bloku a pořadí bloků není známo.

Příklad:

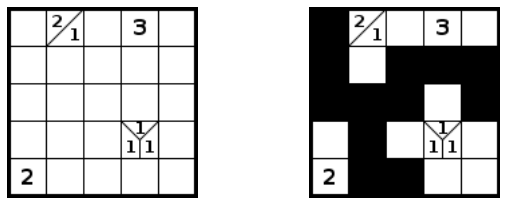
Postup řešení konkrétní úlohy:

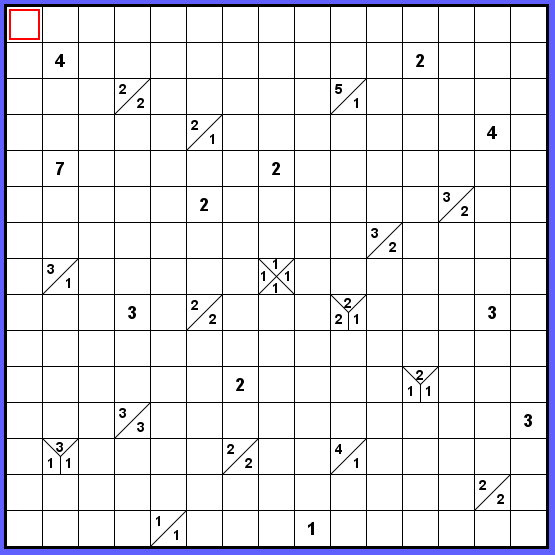
Zadání patřilo do série úloh 15 krát 15, takže je poměrně rozlehlé a spíše těžší, neobsahuje v podstatě žádné obvyklé startovní kombinace čísel.

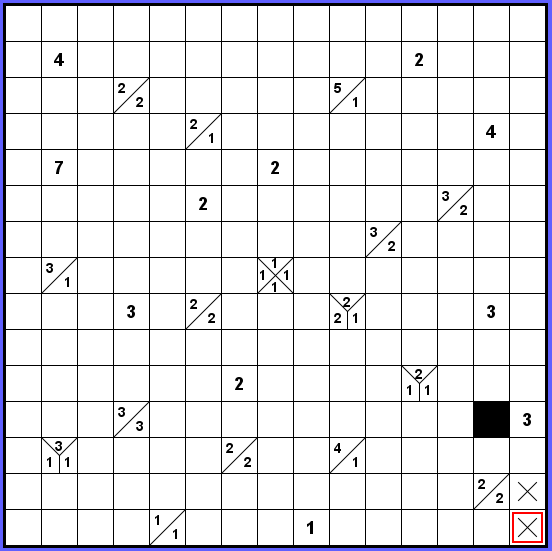
Dvě věci jsou jasné v pravé dolním rohu. Zaprvé nelze využít dvě vykřížkovaná políčka v samém rohu, protože bych již se zdí nevylezl ven. O kousek výš platí, že všechny tři varianty trojky u okraje mají společné jedno políčko, které tedy vybarvujeme.

 

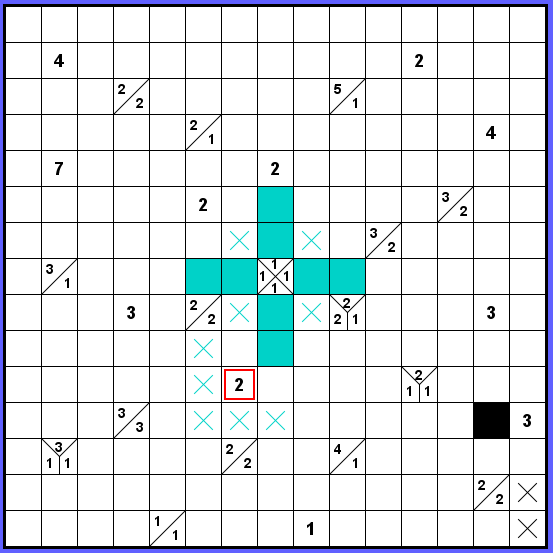
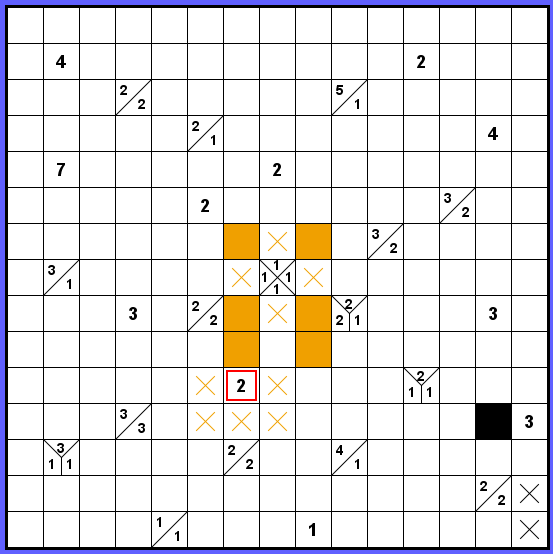
V dalším kroku jsem se z nedostatku jasných kroků zaměřil na prostřední políčko se čtyřmi jedničkami, protože takové zadání umožňuje pouze dvě zcela jasné varianty rozmístění černých políček. Navíc tato políčka vždy musí utéci z obklíčení políček prázdných. A co je podstatné, v obou naznačených variantách se zeď dotkne dvojky (na obrázku s červeným orámováním). Ať už zeď u dvojky pokračuje tam či tam, vždy to znamená několik křížků na opačné straně dvojky.

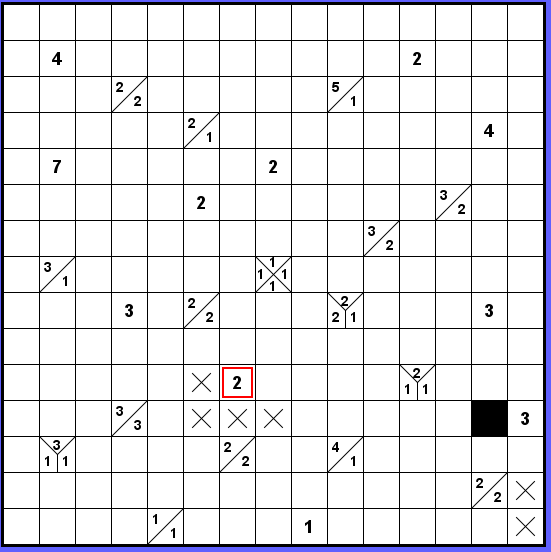
Čtyři křížky jsou společné pro obě varianty a o tento pevný bod opřu další postup řešení.

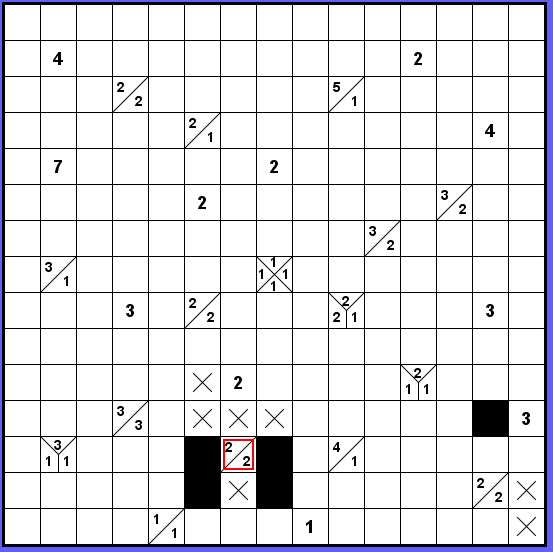
U označného zadání (2-2) totiž zůstává 5 použitelných políček a rozhození na dva-mezera-dva je jasné.

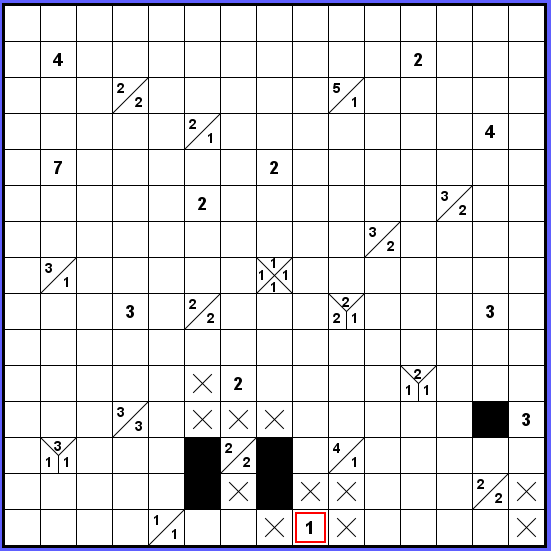
Jedno černé políčko u označené jedničky máme, tedy zbytek bude prázdný.

Taktéž zadání 1-1 při dolním okraji má jednu jedničku splněnou, křížkujeme dvě sousední políčka a s touto částí zdi musíme povylézt ven. Čímž se dotýkáme zadaného políčka 3-3. U něj platí jedna zajímavá věc, jeho okolo musí být středově symetrické, symetricky jsou rozmístěny dvě mezery a také všechna černá políčka. Proto jsem vyčernil políčko naproti tomu, s nímž jsem přišel zespodu.

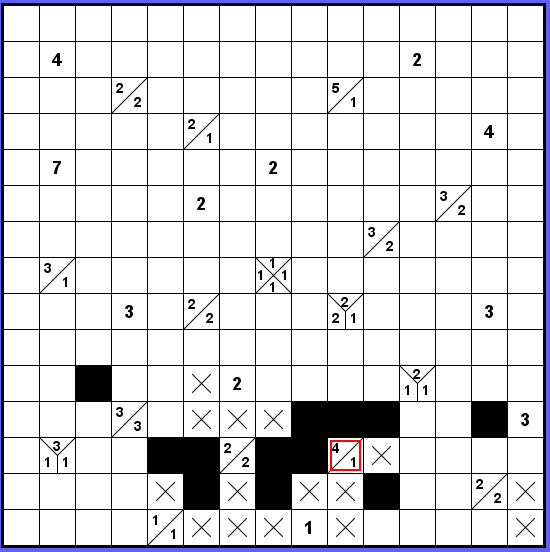
Podobně musím vylézt ven s pravým koncem, který jsem dole načal. Okolí označeného políčka (4-1) je tím dáno.

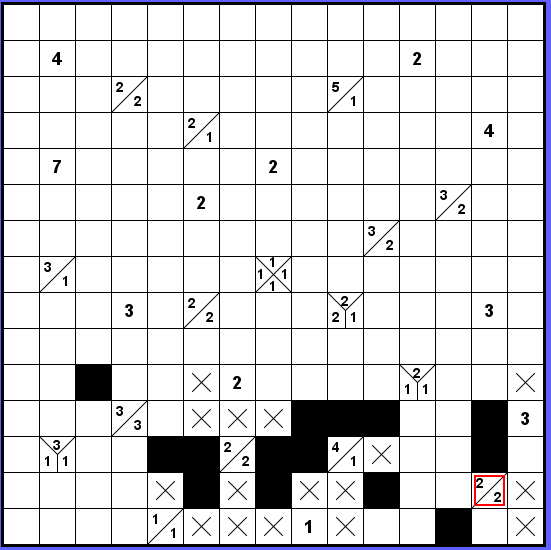
V dalším kroku jsem do okolí označeného 2-2 přidal dvě černá políčka. Proč? Existují čtyři varianty, jak na zbývajících 6 okolních políček rozmístit kombinaci 2-2. Ve všech z nich jsou tato dvě políčka černá. Nebo pohledem z druhé strany — kdyby byla daná políčka prázdná, už by nezbylo dost místa pro dvě dvojky.

Důsledek je, že již mám 2 ze tří políček u trojky na pravém okraji. Proto bude nad ní křížek, tam už by blok délky 3 nedosáhl.

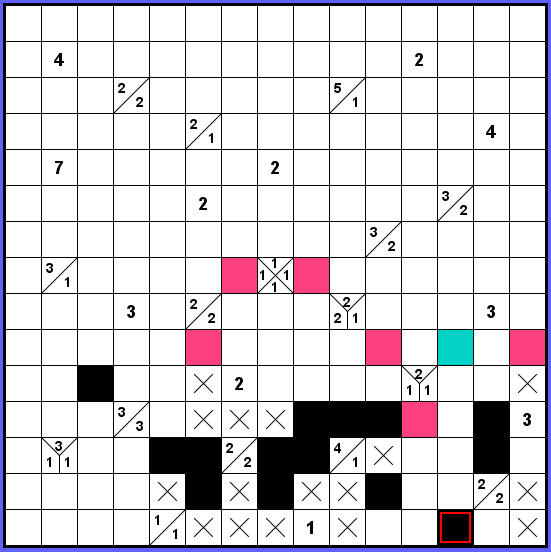
Celým řešením úlohy Tapa se vinou dvě základní úvahy. Ta jednoduší je aplikována v situaci, kdy kolem zadaného čísla zbývá málo možností rozmístění černých bloků, nejlépe možnost jediná. Složitější úvahy se obvykle týkají spojitosti celé zdi. Všechna černá políčka musí být ve výsledku propojená.

Tímto směrem uvažování jsem se pustil nyní. Červeně označený konec zdi se musí nějak připojit do horní části tabulky a ke kamarádům vlevo. Kudy? Nelze projít při pravém okraji (4 políčka okolo 3). Správná varianta průchodu je označena modře. Kdybych se jí chtěl vyhnout, musím projít pod zadaným 2-1-1 a spotřebuji tak z toho dvojku. Pak dojdu pod střed tabulky, ale odtud se nevymotám. Všechny růžově označené průchody by potřebovaly delší černý blok než okolo zadaná čísla dovolují.

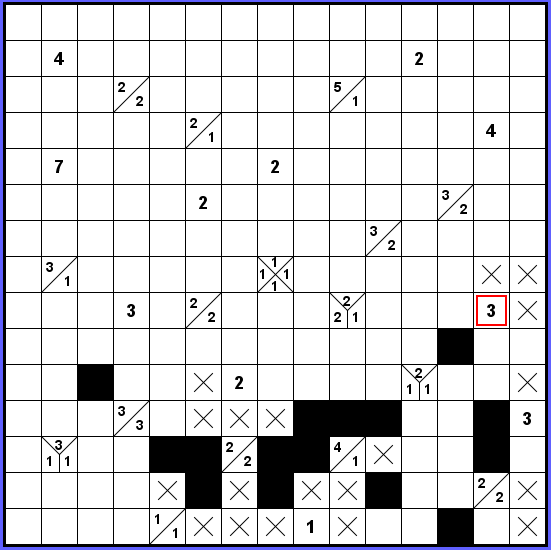
Musíme tedy projít se zdí okolo označené trojky vlevo dole. Na vykřížkovaná políčka v jejím okolí už pak blokem délky 3 nedosáhneme.

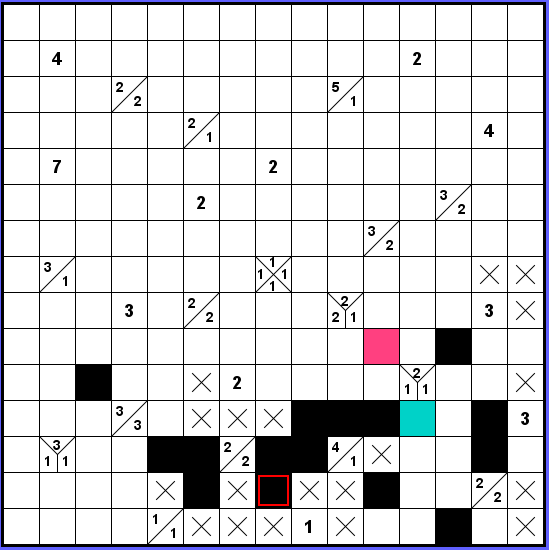
Zjistili jsme před chvílí, že z oblasti pod středem není možné uniknout doleva ani nahoru. Jak tedy vykličkovat s označeným koncem zdi? Nepřipadá v úvahu ani růžově označený průchod. Ve všech variantách bychom vytvořili blok délky 3 okolo zadání 2-2-1, resp. 2-1-1. Jediná volná cesta je označena modře.

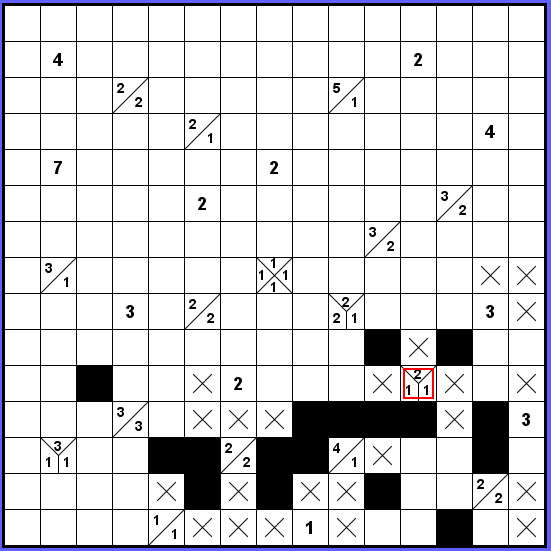
Okolí označeného zadání (2-1-1) je tak již jasně dáno.

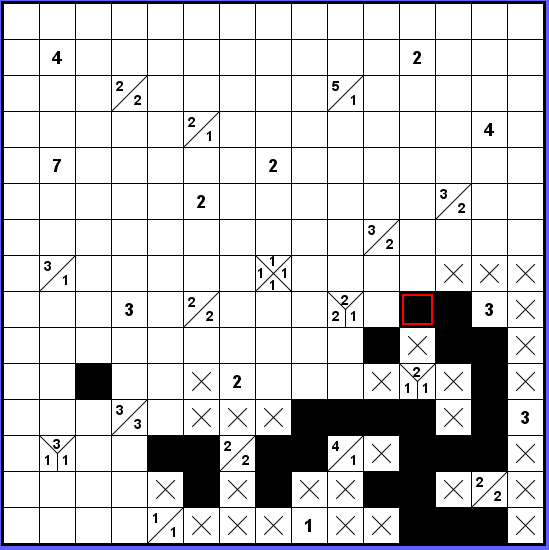
Zeď ze spodní pravé části pak můžeme vytáhnout nahoru až po označené políčko.

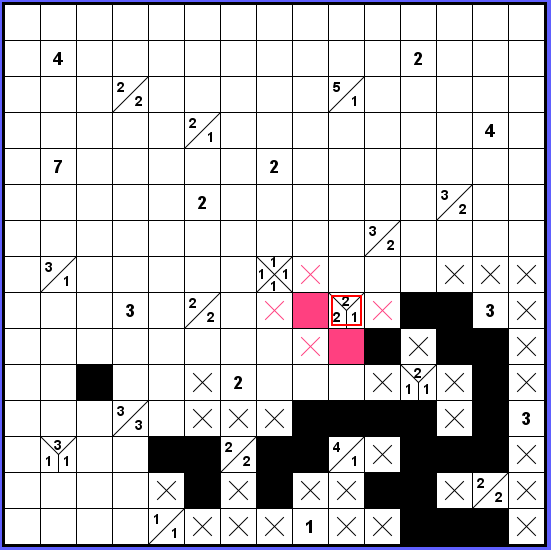
Dále si povšimneme, že zadání 2-2-1 musí být odděleno 3 mezerami a celkově tak máme obsazeno všech 2 + 2 + 1 + 3 = 8 políček okolí. Černé políčko vpravo dole od označeného nemůže být blok délky 1, protože takový by zůstal zcela obklíčený. Tedy dvojka. Ale když se natáhneme vlevo — naznačeno růžově — dostaneme se nalevo od označeného políčka do neřešitelné situace, vznikne osamělý ostrůvek.

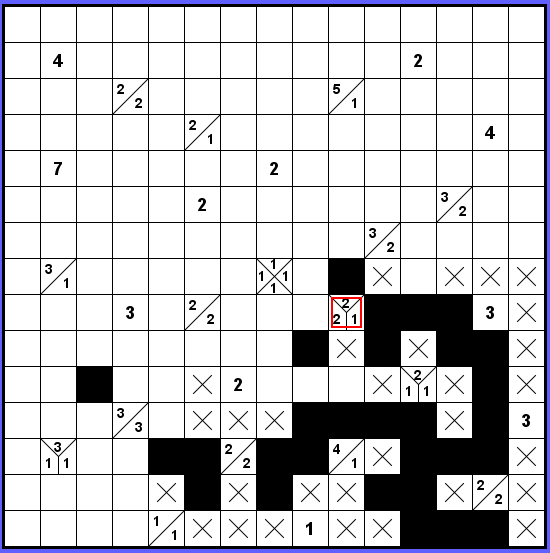
Původní osamělý čtvereček se tedy natáhne nahoru a ve zbytku okolí zadání 2-2-1 můžeme doplnit další dvě políčka. (Protože dle předchozí úvahy o 8 polích v okolí mezery mají délku přesně 1.)

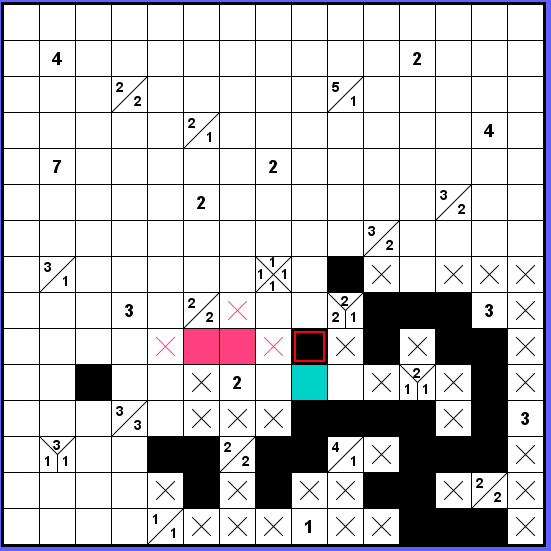
V dalším kroku demonstruji dvě úvahy. Zaprvé se ptám, kudy odejde označený černý čtvereček ze zakleté oblasti pod středem? Jedině přes modré pole, zní odpověď.

Zadruhé si mohu snadno ozkoušet, že růžová varianta dvojky pod středem je nesprávná, zůstává totiž uzavřená, nepřipojitelná.

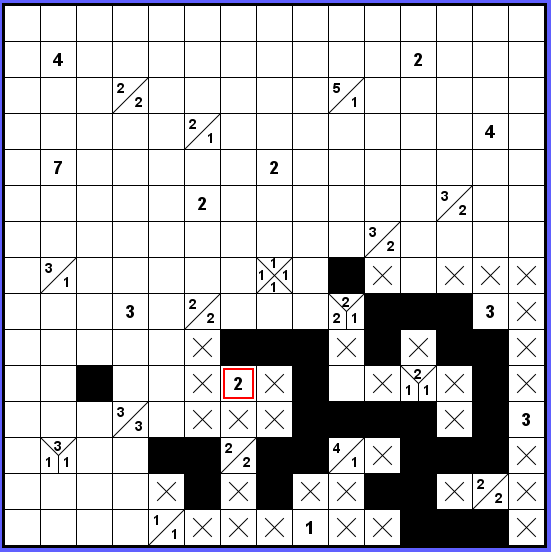
Poté, co připojíme přes modré políčko z předchozího obrázku, zůstává jediná korektní varianta pro označenou dvojku.

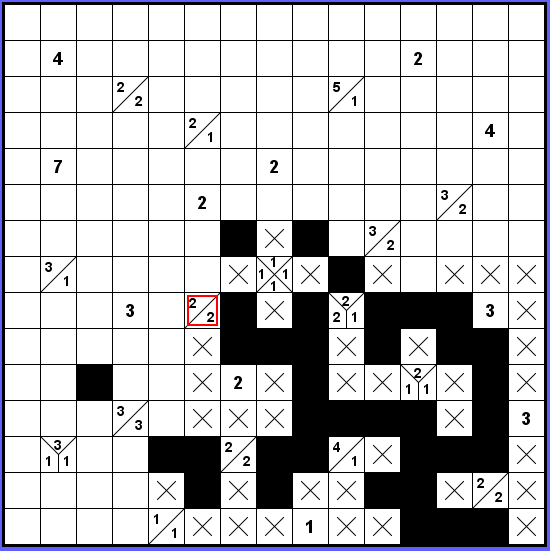
K označenému zadání 2-2 můžeme doplnit jednu dvojku a tím se nám také konečně rozsekne uzel 1-1-1-1 ve středu tabulky.

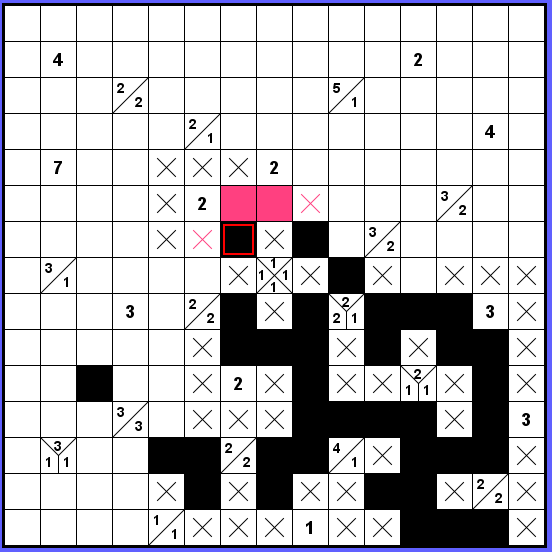
Kam odejdeme s červeně orámovaným dílkem? Doprava to nejde, viz zablokovaná růžová varianta.

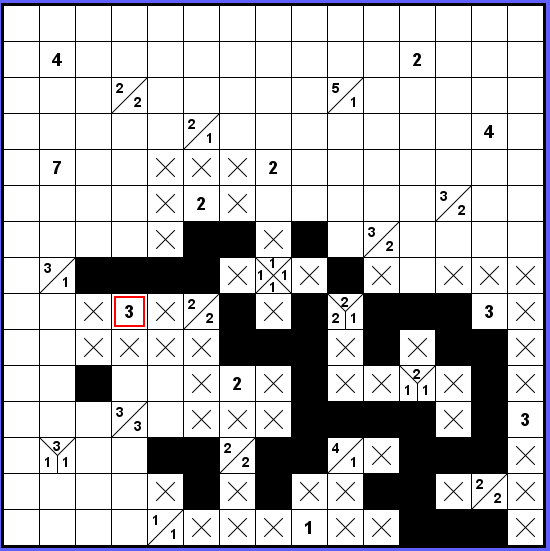
Půjdeme tedy doleva a dojdeme až nad označenou trojku, její okolí i okolí sousedního 2-2 je hotové.

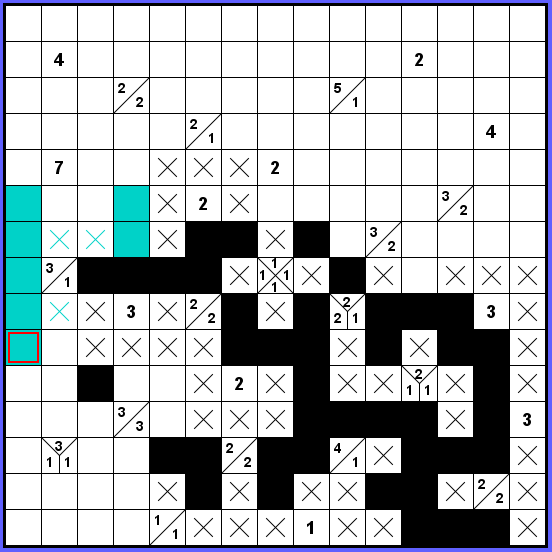
Modře naznačená cesta podél levého okraje tabulky je jediná možnost průchodu z levého spodního rohu do zbytku tabulky. Z okolí zadání 3-1 také plynou další dvě modrá políčka ve čtvrtém sloupci.

Modře naznačený průchod je jediná cesta z levé části tabulky do pravé. Růžový průchod je špatný, potřebovali bychom blok délky 3.

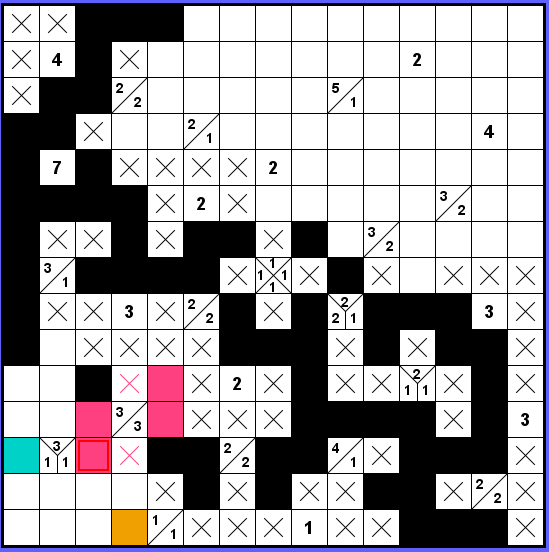
Jak naznačuji oranžově, někde tam bude kus zdi vedle zadání 1-1. Potřebuji s ním projít k ostatním. Správná varianta průchodu je označena modře. Růžová verze s průchodem kolem zadání 3-3 není možná, protože by se část vpravo od 3-3 zablokovala.

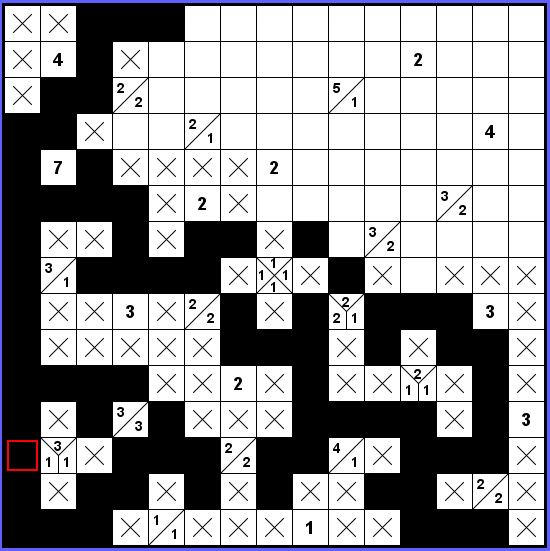
Použitím modrého průchodu z předchozího kroku je kompletně jasné okolí zadání 3-1-1 a s ním i celá levá spodní část tabulky.

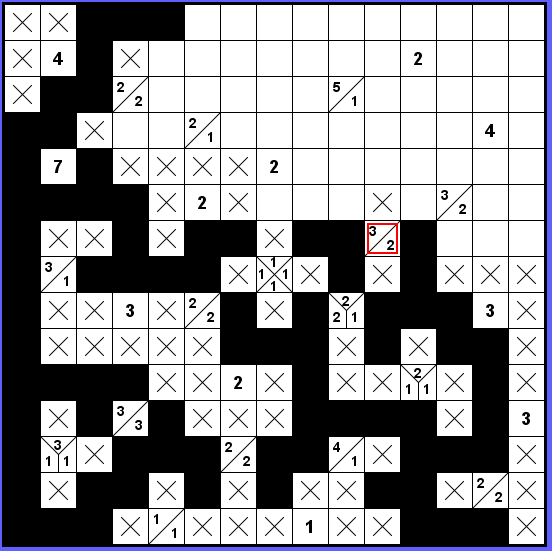
V okolí označeného zadání 3-2 nevíme, zda bude dvojka vpravo, trojka vlevo a nebo naopak. Ale jisté jsou dvě a dvě černé po stranách a jeden křížek nahoře.

 

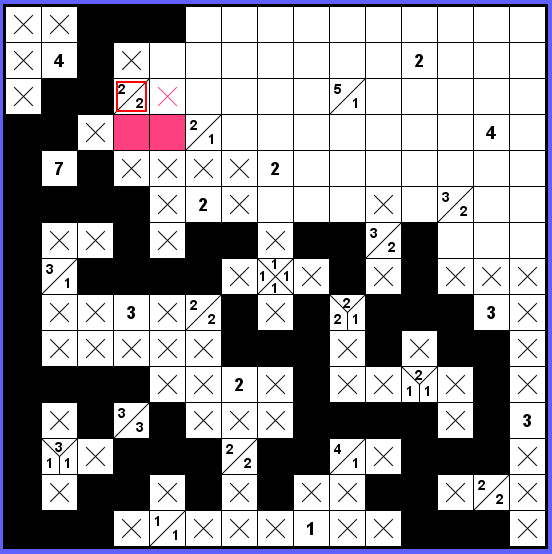
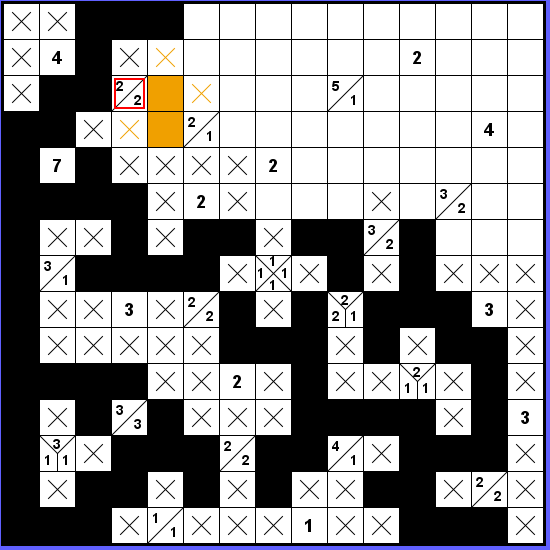
Nyní se zaměříme na druhou dvojku okolo označeného zadání 2-2. Růžová ani oranžová varianta nefunguje, protože skončí zablokovaná.

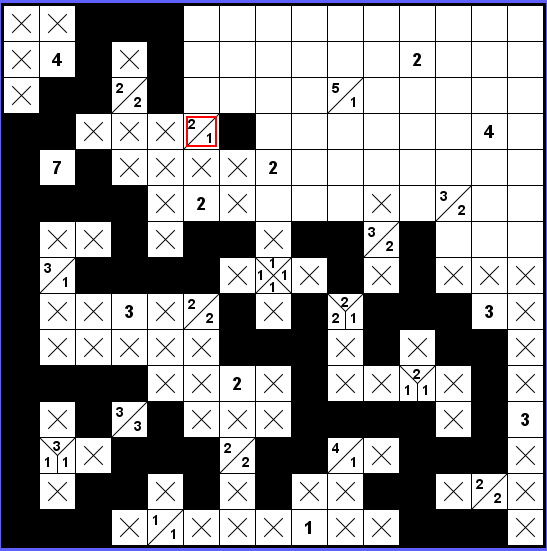
Funguje tedy jedině dvojka nahoře a křížky dole. Což pak způsobí černé políčko napravo u označeného zadání 2-1.

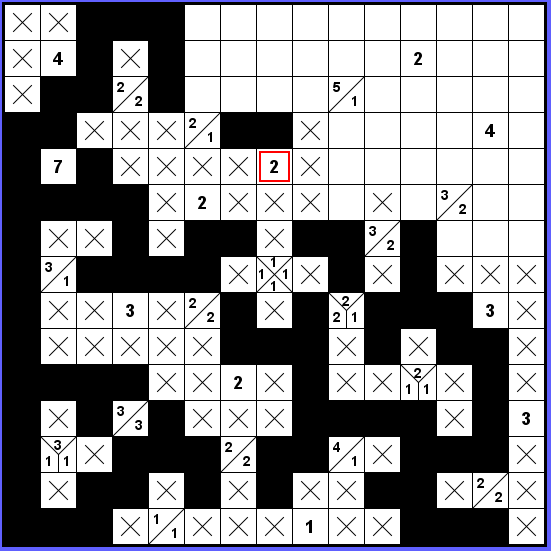
Čímž jsme se posunuli k označené dvojce a dokončíme její okolí.

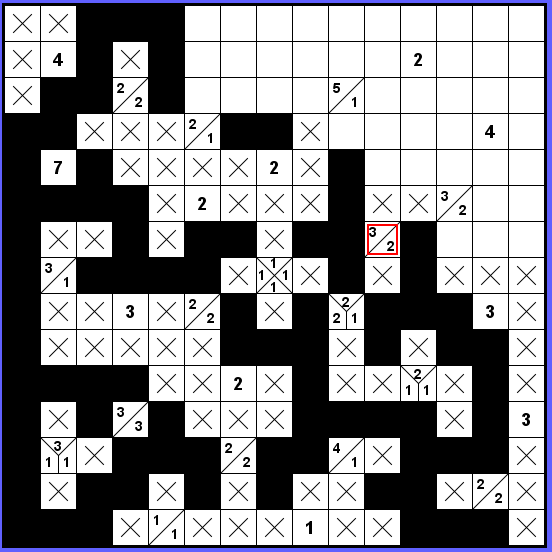
S koncem zdi, který je vlevo od označeného zadání 3-2, musíme ven a máme tedy vlevo trojku a vpravo dvojku.

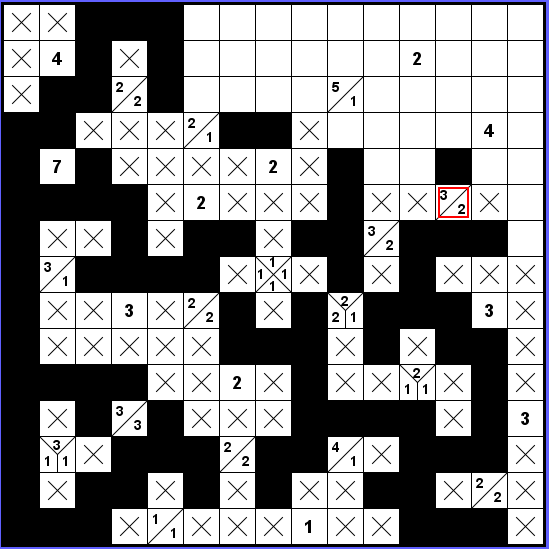
S koncem zdi, který je pod označeným zadáním 3-2, musíme ven. Máme tedy dole trojku a nahoře dvojku, u níž zatím nevíme, zda si vezme levá dvě nebo pravá dvě políčka.

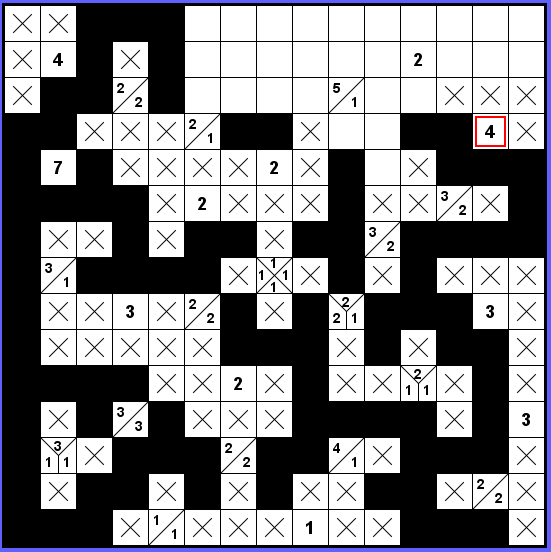
S koncem zdi, který vychází zprava zdola, musíme vykličkovat ven. Abychom zároveň zvládli označenou čtyřku, bude to tak, jak je zakresleno.

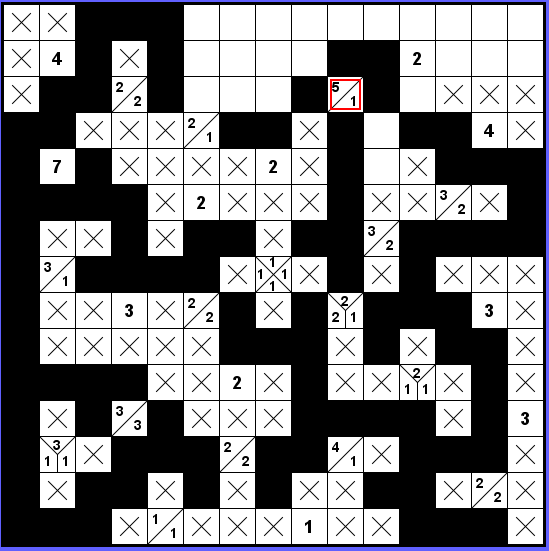
Okolí zadání 5-1 je zajímavé tím, že 5 + 1 + 2 mezery dává 8. Tedy při znalosti mezery vlevo dole, může označit černě úseky 1-3-1 s tím, že se pak jedna dvojice 1-3 propojí do pětky.

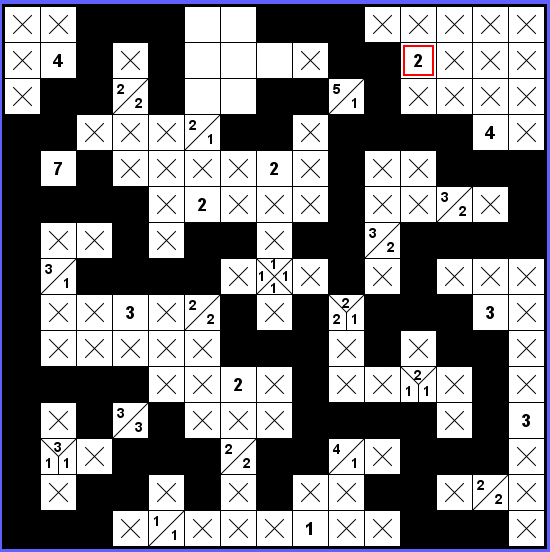
Objevily se nám dvě černá k označené dvojce. Zbytek kolem bude prázdný. Plus propojujeme pravý konec zdi k tomu levému — jedině horem.

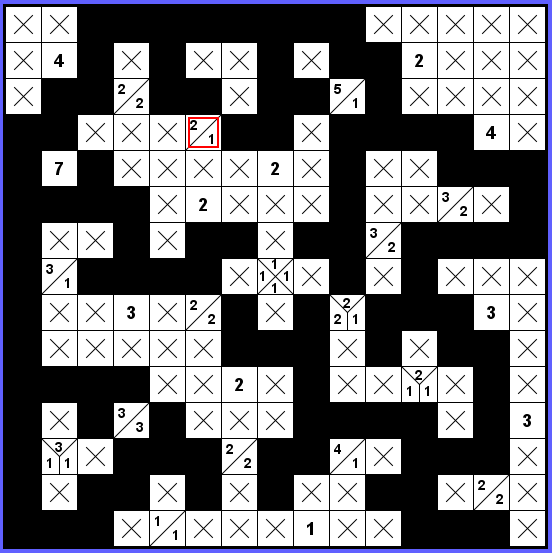
Dokončíme okolí označeného zadání 2-1 a propojení polovin zdi po horním okraji.

Sláva, hurá! Máme to!