Sum of Them Sudoku: návod

Turnaj s názvem Classics vs. Innovatives, který probíhal minulý víkend na serveru logicmastersindia, vzbudil potěšující zájem také u 13 českých hráčů. Možná i proto, že jsme pro vás připravili překlad zadání. Stálo to za to, je příjemné vidět ve výsledkovce česká jména.

Jako v každé soutěži, řešily se úlohy jednodušší i složitější. Caca mě požádal o postup na úlohu Sum Of Them. Napřed jsem se musel trochu smát. Při ostré soutěži jsem totiž spěchal za co nejlepším výsledkem a tuto úlohu jsem vyřešil s trochou štěstí, částečně intuitivně. Na několika místech jsem se spokojil s tím, že určité kombinace vepsaných čísel do sebe dobře zapadají a nepátral jsem důsledně po tom, zda to byla jediná možnost. Také jsem si teprve uprostřed řešení vzpomněl, že číslo v buňce může klidně být součtem tří, nikoliv jen dvou sousedů. Nezabránilo mi to při soutěži v úspěšném vyřešení požadovaných čtyř označených polí a zisku bodů. Pro sepsání postupu bylo potřeba se znovu nad úlohou zamyslet. Zásadní problém to nebyl, i přísně logický postup řešení samozřejmě existuje.

Zopakujme si pravidla úlohy: Čtverečkem jsou označena všechna políčka, kde lze číslo v nich vyjádřit jakou součet vhodné kombinace čísel z polí sousedních. (Hovoří se pouze o polích sousedících stranou.)

A nyní již konkrétní zadání:

Kde vůbec v takto prázdné tabulce začít? Vybral jsem si levý horní čtverec. Je třeba si uvědomit, že při libovolném sčítání platí, že sčítanci jsou menší než součet. Je jasné, že pole R1C1 musí být součtem R1C2 a R2C1. Podle toho jsem si přikreslil značky nerovnosti. Následně R1C2 musí být součtem R1C3 a R2C2 – R1C1 nelze použít, neboť je větší; analogicky R2C1 musí být součtem R2C2 a R3C1 a R1C3 musí být součtem R1C4 a R2C3.

V R1C4 je minimálně 1, pak součet R1C3 = 5, následně R1C2 bude minimálně 6, pokud přičteme opět 1. Zároveň R2C1 je minimálně 3 jako součet 1 + 2. Tedy R1C1 je minimálně 9 = 6 + 3. A více to být nemůže. Čímž máme v levém horním koutě prvních 7 čísel.

Podobným způsobem uvažujeme v levém spodním koutě. R9C1 musí být součtem R8C1 a R9C2, následně R9C2 bude součtem R8C2 a R9C3.

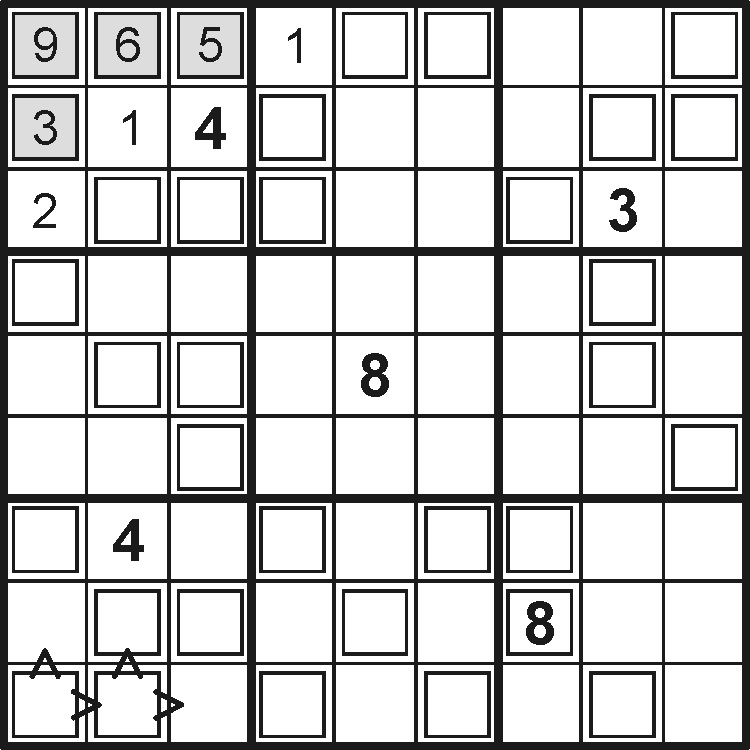
Na pole R8C1 není možné použít 5 (ani vyšší), protože pak by muselo být R9C2 = 3 a nesložili bychom součet v poli R8C2. Píšeme tedy R8C1 = 1.

Na pole R9C2 pak připadá v úvahu 5 nebo 7. První varianta je příliš nízká 5 = 2 + 3 a opět nesložíme součet v poli R8C2. Vychází jedině R9C2 = 7, R9C1 = 8 a součet 7 musíme složit jako 2 + 5.

Doplním ještě, že šedým podbarvením si označuji políčka, kde mám již součet hotový, splněný.

Zahrajeme konečně pár kroků podle sudoku. V první čtverci doplníme 7 a 8. V sedmém čtverci doplníme 6.

Součet R7C1 = 6 můžeme poskládat jako 1 + 1 + 4, 1 + 5 nebo 4 + 2, druhá varianta jako jediná funguje.

Rozhodnout o umístění 3 a 9 v sedmém čtverci také lze, součet R8C3 = 3 by nebylo možné složit, proto R8C3 = 9 a R7C3 = 3.

Číslo 1 nemůže být součtem dvou čísel, proto ve třetím sloupci bude R4C3 = 1 a následně R6C3 = 8 a R5C3 = 6 umístíme podle sudoku.

Podobně v druhém sloupci součet R5C2 nemůže být 2 ani 3, proto vepisujeme 9. Následně vidíme, že R5C3 bude součtem R4C3 a R5C4, a píšeme R5C4 = 5.

Na jiném místě tabulky je možné doplnit R3C9 = 1 jako jediné možné umístění čísla 1 ve třetím čtverci.

Ve třetím řádku ještě dořešíme součet R3C3, z možností 7 = 4 + 1 + 2, 7 = 4 + 3, nebo 7 = 1 + 6 funguje jen ta poslední.

Ještě v pravém horním koutě se můžeme odpíchnout od rohového políčka. Bude platit, že R1C9 = R1C8 + R2C9 a R2C9 = R2C8 + R3C9.

V druhém řádku připadá v úvahu jako minimální možnost 6 = 5 + 1, pak přičteme R1C8 = 2 a máme R1C9 = 8 jako minimum a zároveň maximum. Je to tedy jediná možnost, jak vyplnit čísla v pravém horním koutě.

Ze sudoku dohráváme R4C8 = 8.

Někde v prvním řádku musí být číslo 3, zároveň složené jako součet 1 + 2. Při následném rozhodování o umístění 4 a 7 v prvním řádku vyjdeme z toho, že součet R1C6 = 4 bychom nesložili.

Čísla 7 a 9 ve třetím čtverci umístíme podle sudoku.

V tuto chvíli jsem poprvé použil negativní podmínku. Vzhledem k tomu, že v zadání je řečeno, že všechny součty jsou označené, není možné, aby bylo R2C6 = 9; součet by platil a čtvereček nikde. Proto můžeme doplnit čísla 8 a 9 ve druhém řádku. (A součet R2C4 = 9 pak vyjde ze tří polí 9 = 6 + 2 + 1.)

Dostali jsme se k tomu, že součet R3C4 musí vzniknout jako R3C5 + R4C4. Z možností 6 = 3 + 3, 6 = 1 + 5, nebo 6 = 2 + 4 funguje pouze ta poslední ve vhodném provedení.

Doplňujeme 4 a 5 ve druhém čtverci, 2 v pátém čtverci a pak podle sudoku také 2 a 3 ve čtvrtém čtverci.

Ve čtvrtém čtverci nyní můžeme jediným způsobem umístit 4 a 7 tak, aby fungoval součet R4C1.

Ve čtvrtém sloupci zbývají čísla 3, 4 a 7. R6C4 nemůže být 3, protože by se na pozici R5C4 objevil součet 5 = 2 + 3 bez označení čtverečkem. Zároveň nemůže být R8C4 = 3 protože by v žádné kombinaci nefungoval součet R8C3. Vychází nám tedy jedině R9C4 = 3 a doplňujeme také R9C5 = 1 ze součtu 3 = 2 + 1.

Následně můžeme doplnit 1 a 3 dle sudoku v devátém čtverci.

Podíváme se na zbývající dvě trojky. Na pozici R5C6 totiž nemůže být 3, protože by se na pozici R5C5 objevil součet 8 = 5 + 3 bez označení čtverečkem.

Musí tedy být R6C6 = 3, doplníme zbývající trojku, dvě jedničky, tři dvojky a dvě sedmičky, vše podle sudoku.

Poslední krok před klasickou dohrávkou je zjištění, že pro pole R6C8 ze tří možností 4, 6, nebo 9 pouze ta první úspěšně doplní součet R5C8 = 7 = 3 + 4. Zbývající čísla doplníme podle sudoku.

A je to!

S pozdravem! Honza Krtek Novotný