Návod na šošony

Zadání první úlohy

Při cestě dolů labyrintem umísti postupně písmena ze slova Š-O-Š-O-N, v tomto pořadí za sebou, a to přesně 3x. Mezi jednotlivými písmeny může být prázdné pole. Do polí s čárkou již nelze umístit žádné písmeno. Zároveň musí platit, že v každém řádku a sloupci se nesmí žádné písmeno opakovat. Navíc se žádné z písmen nesmí dotýkat jiného stejného písmene, a to ani diagonálně.

Do labyrintu máme umístit 3x slovo ŠOŠON, tj. 6x písmeno Š, 6x písmeno O, 3x písmeno N, aby se žádné z písmen neopakovalo v žádném řádku či sloupci. Tudíž v každém řádku a sloupci se písmena Š a O vyskytují právě jednou. V třetím řádku jsou pouze tři možnosti, kam umístit písmena Š a O a z toho plyne, že v 2ř2s a 4ř2s nemůžou být tato písmena z důvodu, že by se dotýkala stejných písmen v třetím řádku. Taktéž na těchto dvou pozicích (2ř2s, 4ř2s) nemůže být ani písmeno N, jelikož bychom od vchodu do labyrintu nebyli schopni umístit před ním písmena ŠOŠO bez toho, aniž by se stejná písmena navzájem nedotýkala. 

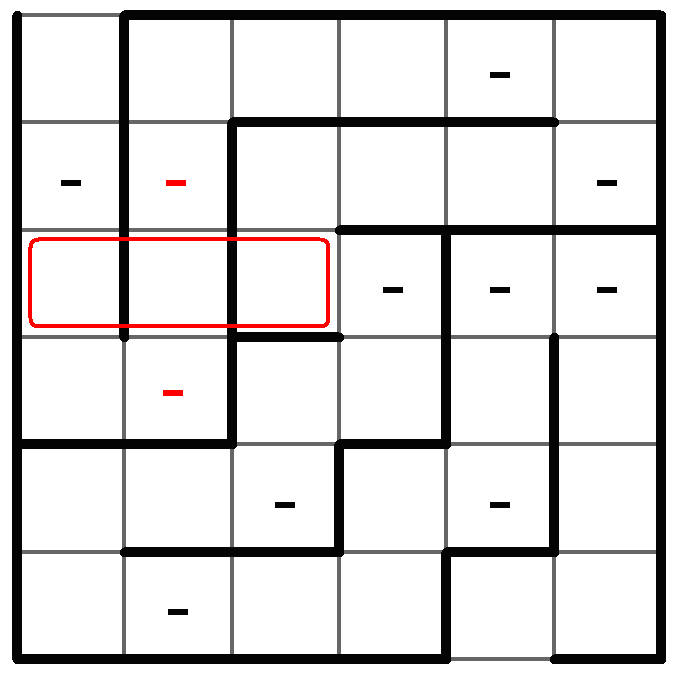
V dalším kroku se pokusíme o umístění písmen Š a O. V pátém sloupci jsou tři volná pole, z nichž dvě budou obsazeny písmeny Š a O, v políčku nejvíce vespod (6ř5s) být Š ani O nemůže, pokud by pole obsahovalo písmeno, tak jedině N. Zbylá dvě volná pole si označím z praktických důvodů jako A a B, protože nevím, které z písmen je Š a které je O.

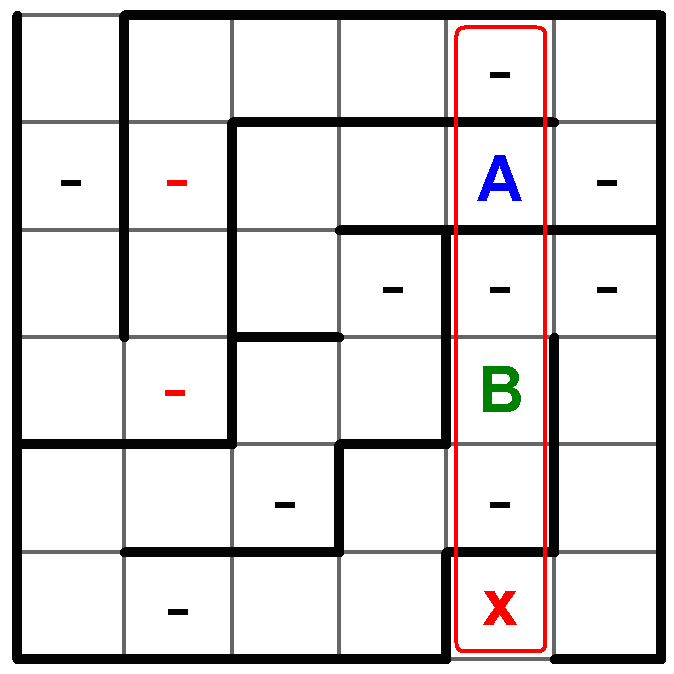
Na základě pravidla, že se stejná písmena nemůžou dotýkat ani rohem, si označím, která pole nemohou obsahovat písmeno B. Dále postupuji tak, že si označím pro všechny řádky možné pozice, kde písmeno B může být:

v 5. řádku pouze na pozici 1 a 2

v 2.řádku pouze na pozici 3 a 4 -> z toho plyne že nemůže být B na 3ř3s

v 3.řádku tak pouze na pozici 1 a 2

v 1. řádku z toho plyne B pouze na pozici 6

a v 6.řádku na pozici 3 a 4

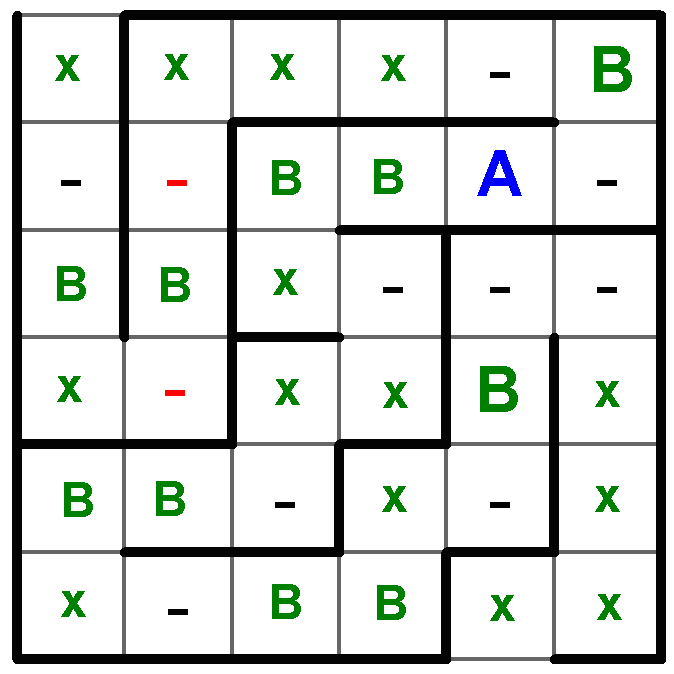
Na základě stejného pravidla si doplním možné pozice písmene A. Dále také vím, že mezi každým písmenem B se během cesty labyrintem musí nacházet právě jedno A, z toho plyne:

ve 4.sloupci se A musí nacházet na pozici 5 nebo 6, tj. mezi dvěma písmeny B

v 1.sloupci se A taktéž musí nacházet na pozici 5 nebo 6

v 6.sloupci na A zbývá pozice 4

mezi 3. a 4. písmenem B při cestě labyrintem může být A pouze na pozici 3ř3s

a v 2. sloupci může pak být písmeno A pouze na pozici 1

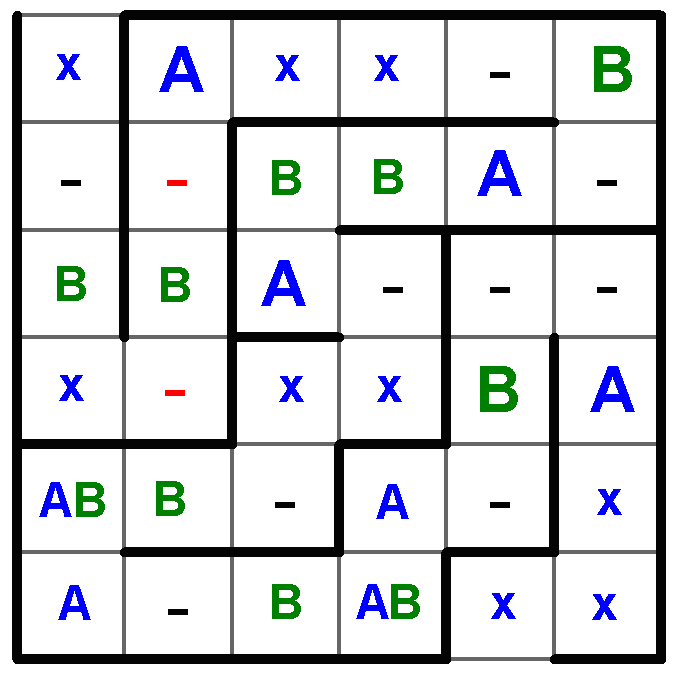
Při cestě labyrintem se nachází první písmeno B, které tedy představuje Š, písmeno A pak představuje O.

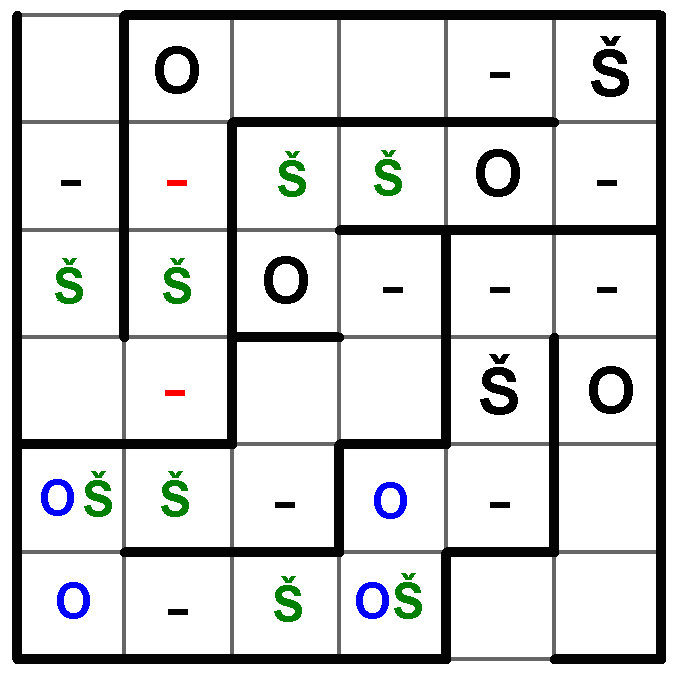
Dále víme, že po každém druhém písmenu O musí následovat N. Doplňme tedy:

na 2ř4s písmeno N -> z toho plyne

na 2ř3s písmeno Š -> z toho plyne

na 6ř4s písmeno Š -> z toho plyne

na 5ř4s písmeno O -> z toho plyne

na 6ř1s písmeno O

v 3.řádku může být pak Š pouze na pozici 1

a v 5 řádku může být pak Š pouze na pozici 2

do volného pole na na pozici 6ř3s doplním druhé N

a třetí N může být jen na pozici 5ř6s

A hurá na cestu labyrintem zpět!

Zadání druhé úlohy

Při cestě nahoru labyrintem umísti 3 šošoní spojení – CACA, DICARLO, JZVERINA - tak, že každé z uvedených spojení se musí nacházet v labyrintu v polích za sebou, tj. nemůže být mezi nimi prázdné pole vyjma prázdných polí již zadaných. Mezi jednotlivými spojeními prázdné pole být může. V jakém pořadí se v labyrintu nacházejí, předem neznáte. Do polí s čárkou již nelze umístit žádné písmeno. Zároveň musí platit, že v každém řádku a sloupci se nesmí žádné písmeno opakovat. Navíc se žádné z písmen nesmí dotýkat jiného stejného písmene, a to ani diagonálně.

Klíčové je umístění spojení CACA, ve kterém se opakují písmena C a A. Při průchodu labyrintem musí být tato písemna od sebe oddělena alespoň jedním dalším polem, jinak by se nejméně jedno z písmen dotýkalo jiného stejného písmene. Využijme tedy míst v labyrintu s již zadanou čárkou, pak lze spojení CACA do labyrintu umístit dvěma způsoby. 

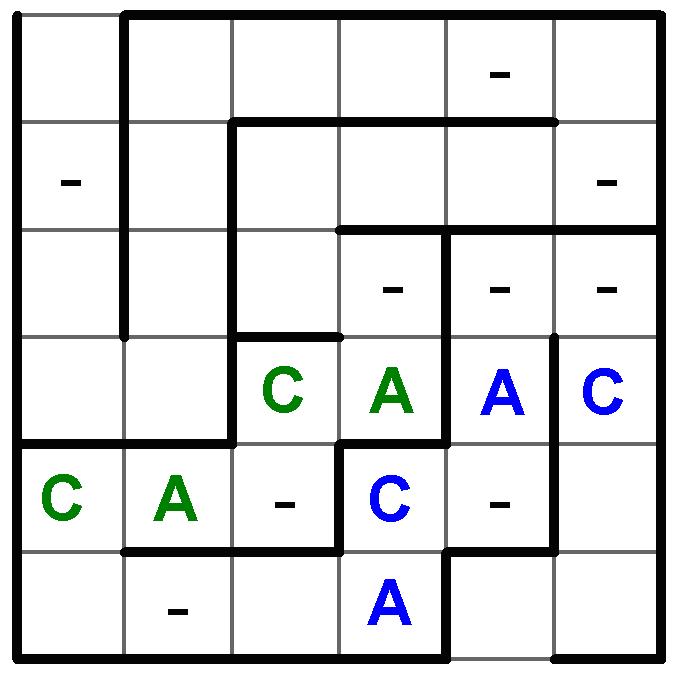
V první zelené variantě (podle obrázku) nelze před spojení CACA zadat ani jedno z dvou zbylých spojení, jelikož písmeno A se v těchto spojeních nachází na čtvrté, respektive osmé pozici, a tyto pole jsou již „v dosahu“ písmen A ze slova CACA. Obě zbylá spojení mají celkem 15 písmen (7+8=15), ale volných polí za spojením CACA zbylo jen 14, sem je nelze také zapsat.

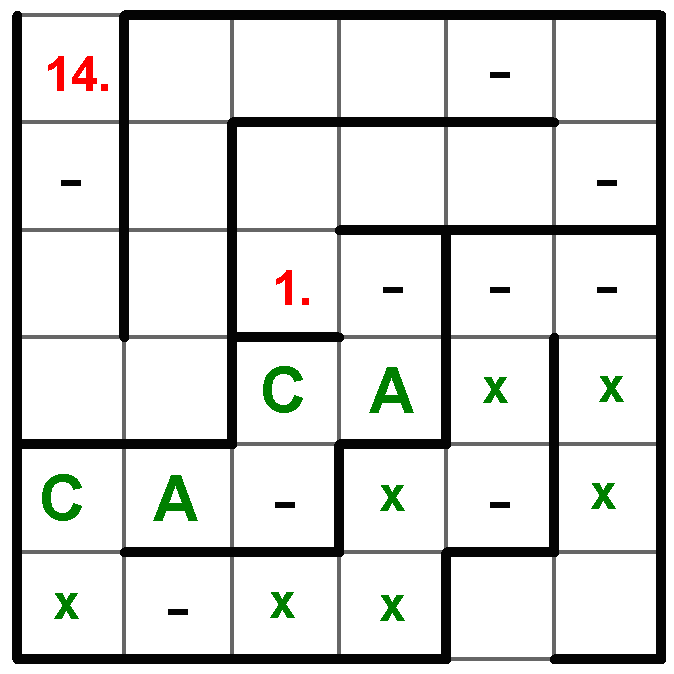
Do labyrintu tak musíme zapsat spoejní CACA podle umístění modré varianty. Pro umístění zbylých spojení nechť využijme přítomnosti dalších stejných písmen ve spojeních, a to písmene I a R ve spojení DICARLO a JZVERINA a písmen CA ve spojeních CACA a DICARLO. Písmeno C ze spojení DICARLO můžeme umístit do labyrintu pouze na pět pozic. Ostatní pozice jsou „v dosahu“ již zadaných písmen C či je nelze umístit kvůli následujícímu písmenu A ze stejného důvodu.

Umístění spojení DICARLO podle prvního C (pozice 3ř3s) by nám znemožnilo následné umístění spojení JZVERINA v polích před ním, protože jsou dostupná jen 4 pole, i za ním, z důvodu přítomnosti dvou písmen I na 4. řádku v obou spojeních. Druhé možné umístění písmene C (pozice 2ř5s) by způsobilo nedostatek volných polí v místech před i za spojením pro následné umístění spojení JZVERINA (tj. 7 volných polí před a 6 volných polí za spojením pro osmipísmenný výraz). Pro zbylé tři možná umístění výrazu DICARLO si zapíšeme pozice písmen I a R (na obrázku červeně), jelikož ty následně můžou vyloučit pozice písmen I a R ve spojení JZVERINA (na obrázku zeleně). Písmena A ze spojení CACA zredukovala možnost zapsání výrazu JZVERINA pouze na dvě pozice.

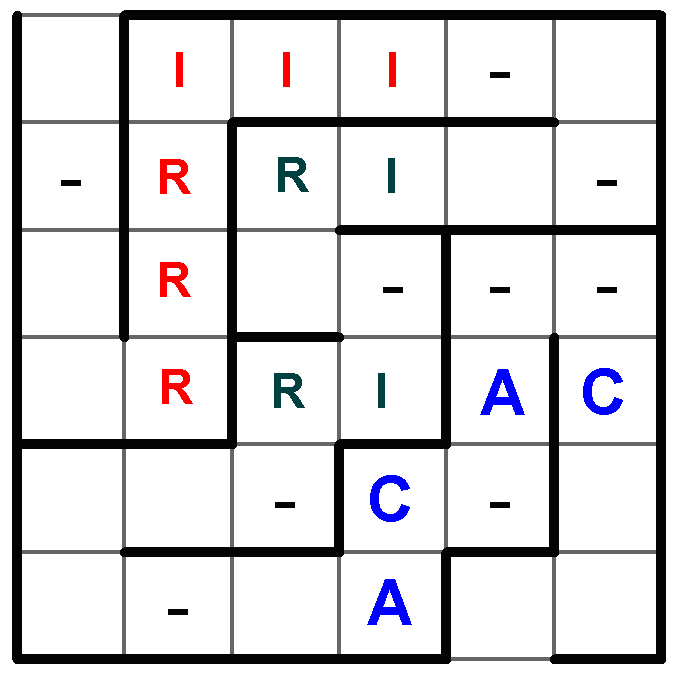
Písmeno R ze spojení DICARLO na 3ř2s by znemožnilo zapsání obou zbylých variant výrazu JZVERINA a naopak přítomnost písmene I ve 4.sloupci ze spojení JZVERINA omezuje zapsání možnosti umístění spojení DICARLO s písmenem I na pozici 1ř4s. Vychází tak jediná možnost pro zapsání obou zbylých výrazů.

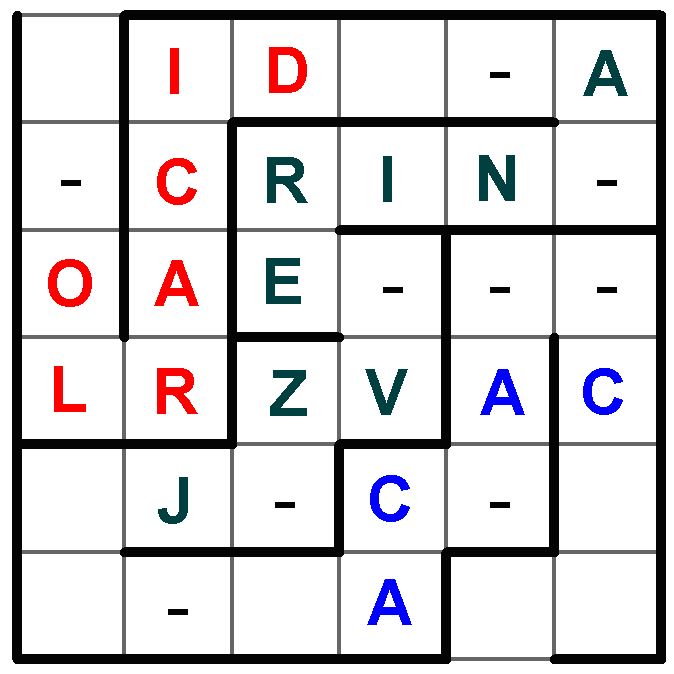
A máme hotovo 

Pavel Kadlečík