Ročenka 2015: Postup pro úlohu L9

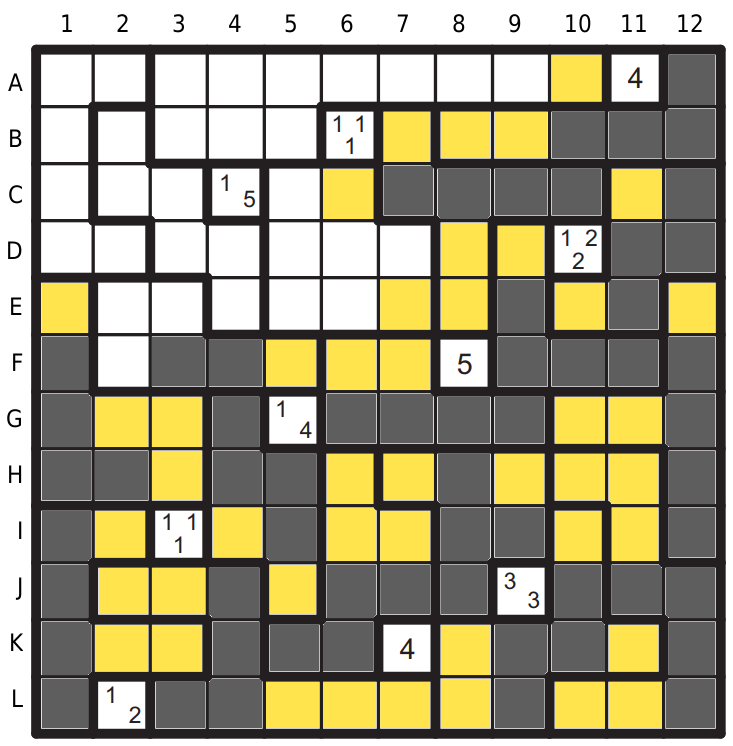
Začneme u (4) v poli A11 – začerníme tři políčka na druhém řádku B10,B11,B12. Ve stejné oblasti je mezera na B8, až sem tetromino určitě nedosáhne.

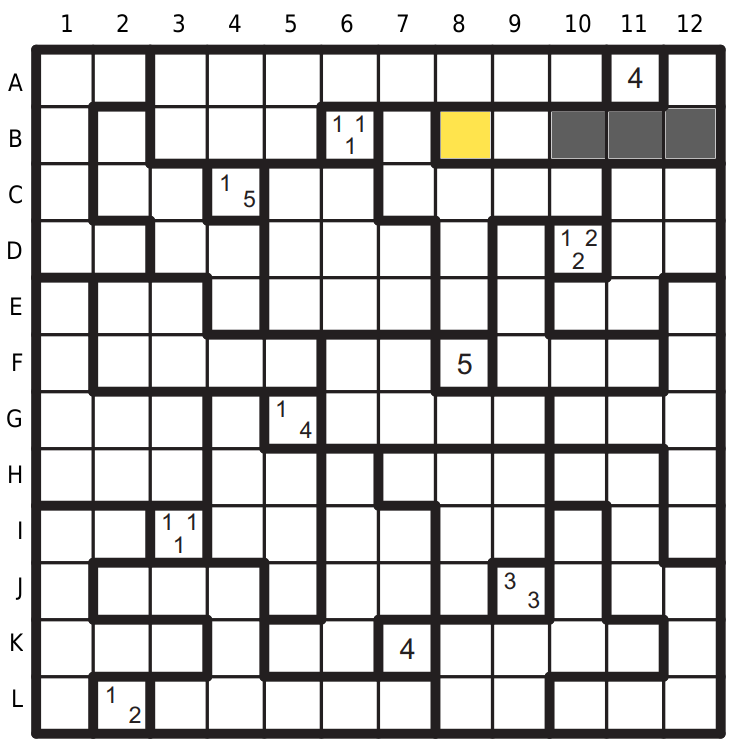
Oblast D9 určitě vyplní roh E9, F9, F10. Mezera na E10, jinak máme černou oblast 2x2.

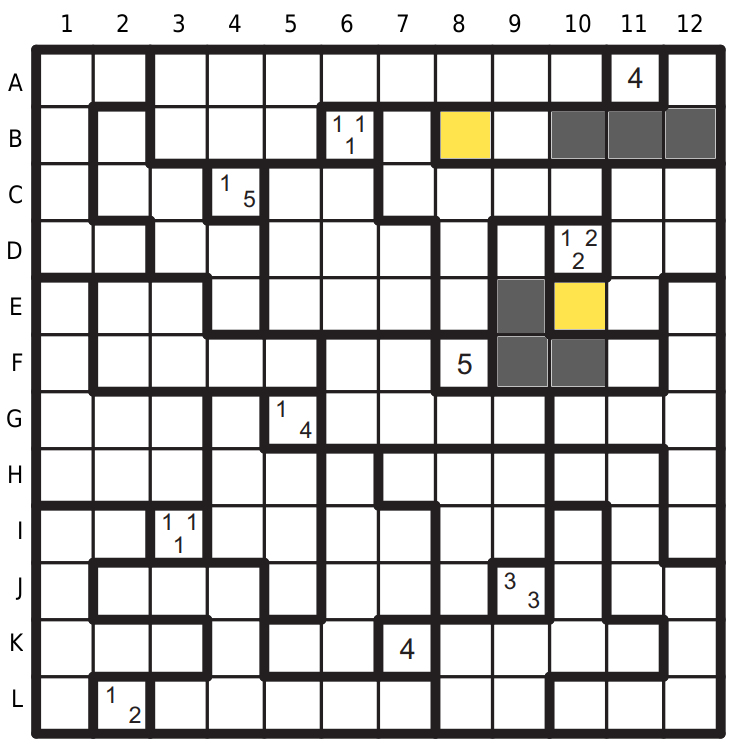
Oblast C11 určitě obsadí pole D11,D12 a E11, protože na C11 a C12 může být jenom jedno pole černé.

A aby platila i tapa D10 (1-2-2) bude to pole C12, automaticky doplníme mezeru na E12.

Pokračujeme tapou na D10, zbývají nám 4 pole na (1-2), tudíž musíme začít od kraje – černá C10, doplňujeme tetromino (C9, C8), mezera B7, E8. Mezera v tapě na D9, černá F11.

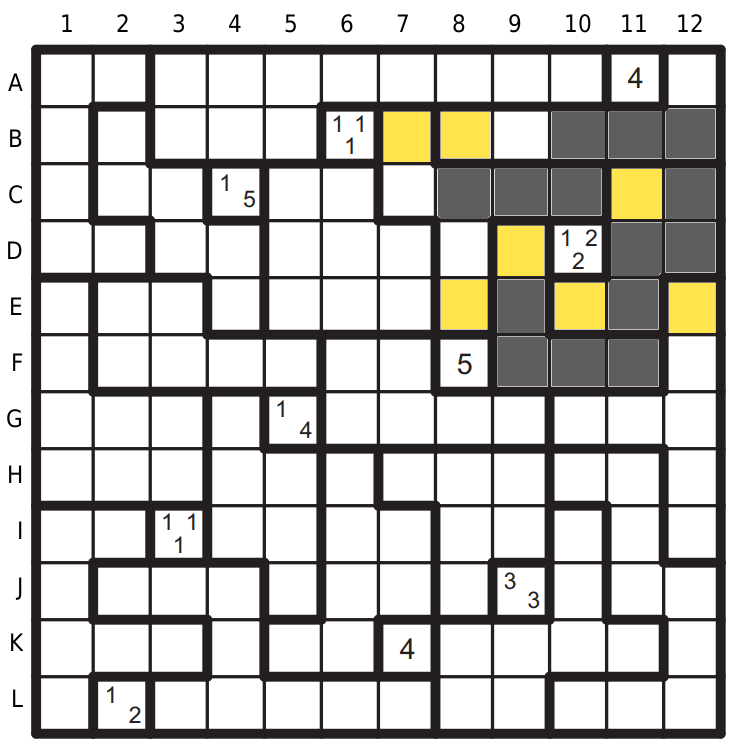
Nemůžeme mít pole 2x2 celé černé, proto je mezera na B9, G10. Doplníme tetromino A12, sousedící oblast nesmí být L, takže je černá na C7, mezera na A10, D8 a C6 (1-1-1). Doplníme podle F8 (5)  černá G9, G8, G7, mezera F7, E7 a tetromino I v oblasti F6.

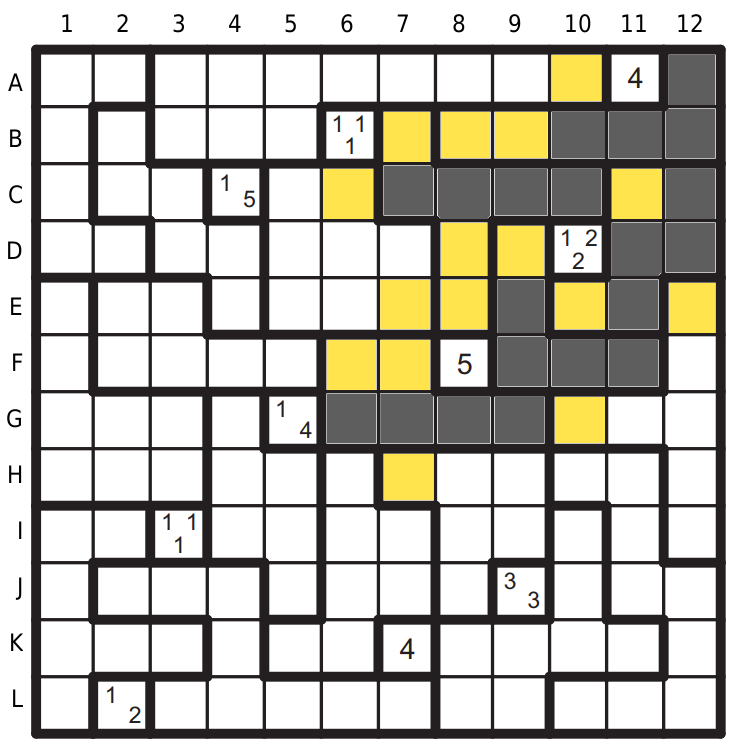
V oblasti E12 doplníme tetromino I, protože S se tam nevejde, T by vytvořilo černou oblast 2x2 a L je v sousední oblasti. V oblasti H10 potom mezery na H10, H11, I11 (jinak máme černé 2x2) a potom bude určitě černé pole K12 a L12 a určitě tetromino L, jenom zatím nevíme jak orientované. Vždy ale zablokuje pole K11.

V oblasti H7 nám zbývá 5 polí ve tvaru písmene P, protože tetromino O není dovoleno, určitě bude  černé J8 a I8. Navíc v oblasti I10 bude mezera na I10, protože tapa na J9 je jenom (3-3), a když máme tuto mezeru, doplníme vše okolo J9, tetromino S do oblasti I10.

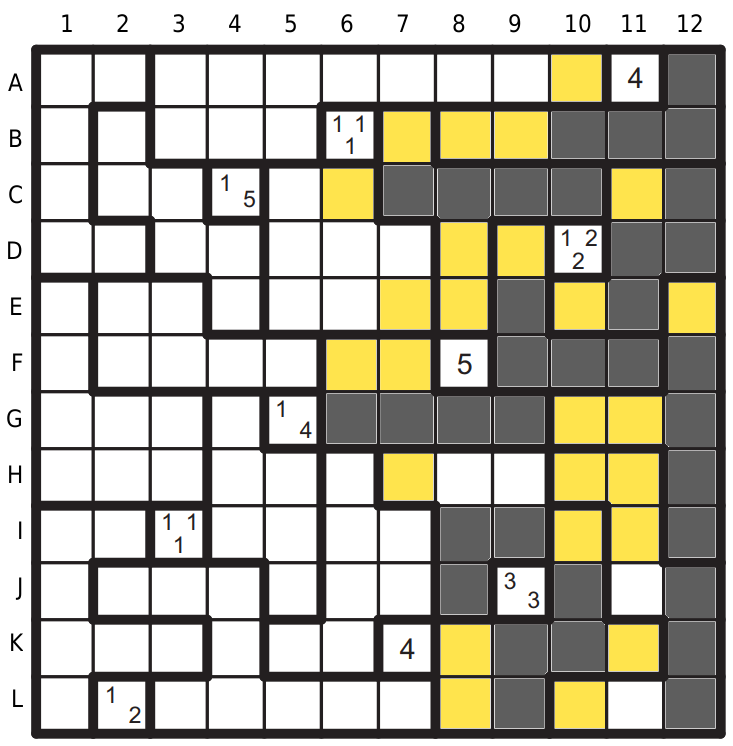
Pokračujeme tapou kolem K7,  v oblasti H10 doplníme tetromino, tak aby se propojila oblast I10 se zbytkem.

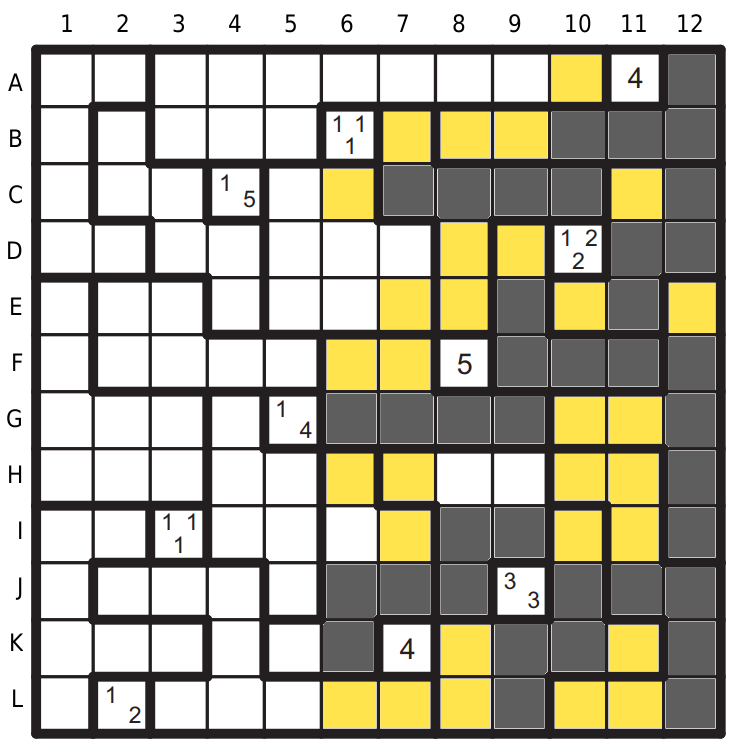
Tapa G5 zbývá (4), určitě bude černé F4, G4, H4,. Tapa na I3 (1-1-1) nutí mezeru na H3 a I4, doplníme tetromino S v oblasti G4. Tapa G5 je celá, na F5 je tudíž mezera.

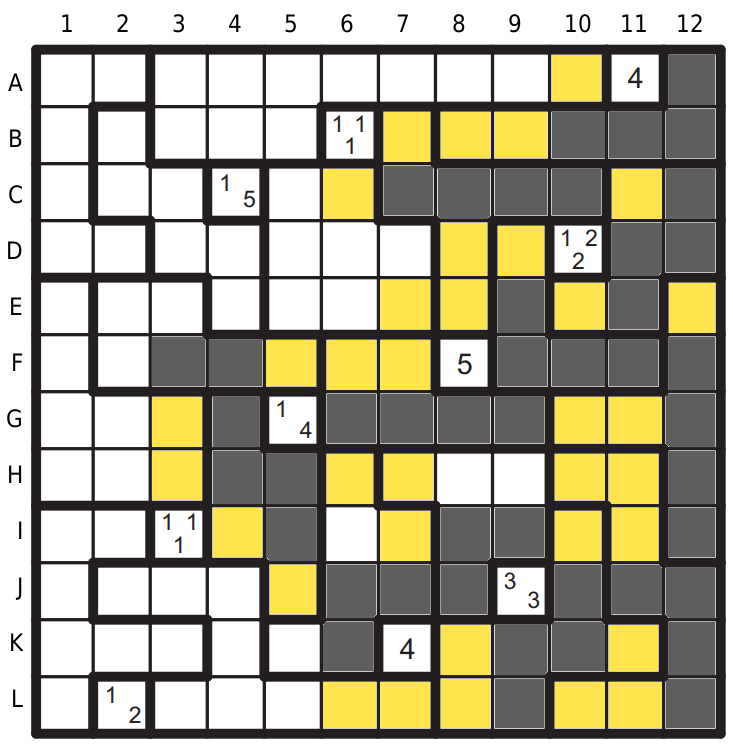
Tapa na I3 (1-1-1) nutí mezeru na J2 a J3, černou J4, K4, L4. K3 je mezera, protože tetromino odsud by porušilo tapu L2. A aby platilo L2 (1-2) bude L3 černé, L5 mezera, oblast J2 pak musím propojit se zbytkem, proto je K5 černá, I6 mezera a máme tetreomino S. Sousední  tetromino v oblasti H7 musí být tudíž T.

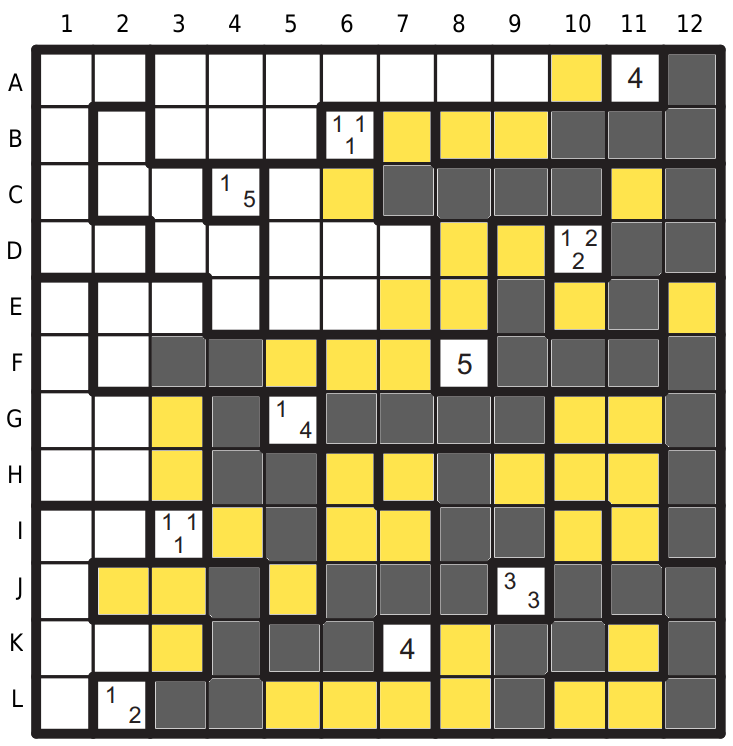
V oblasti I1 bude tetromino I nebo L, protože potřebuji dvě pole kolem L2, mezera na I2 a černé H2. Aby byla oblast I1 propojená, musí být černé H1, doplním tetromino L, jiné se nevejde a tedy v oblasti I1 bude I.

Propojuji dál, černá F2, oblast E2 sousedí s L, takže doplňuji na T a mezeru na E4. V oblasti B2 bude určitě S přes C2, C3 a D3, to nutí mezeru na D2. Oblast A1 tak orčitě obsadí A1, A2 a A3. Mezera na B2, černá D4.

Tapa B6 (1-1-1) nutí začernit pole C5, protože dvě jedničky v jedné oblasti (A3) neudělám. Pokračuji černou D5,  doplním podle C4 mezeru na B3, B5, černou na B4. Abych neporušil tapu na B6 se v oblasti A3 vejde pouze tetromino T na A3, A4 a A5, mezery na A6 až A9.

Nyní zbývá už jenom pospojovat černé oblasti dohromady přes A2 a D6, D7. A JE TO !!!