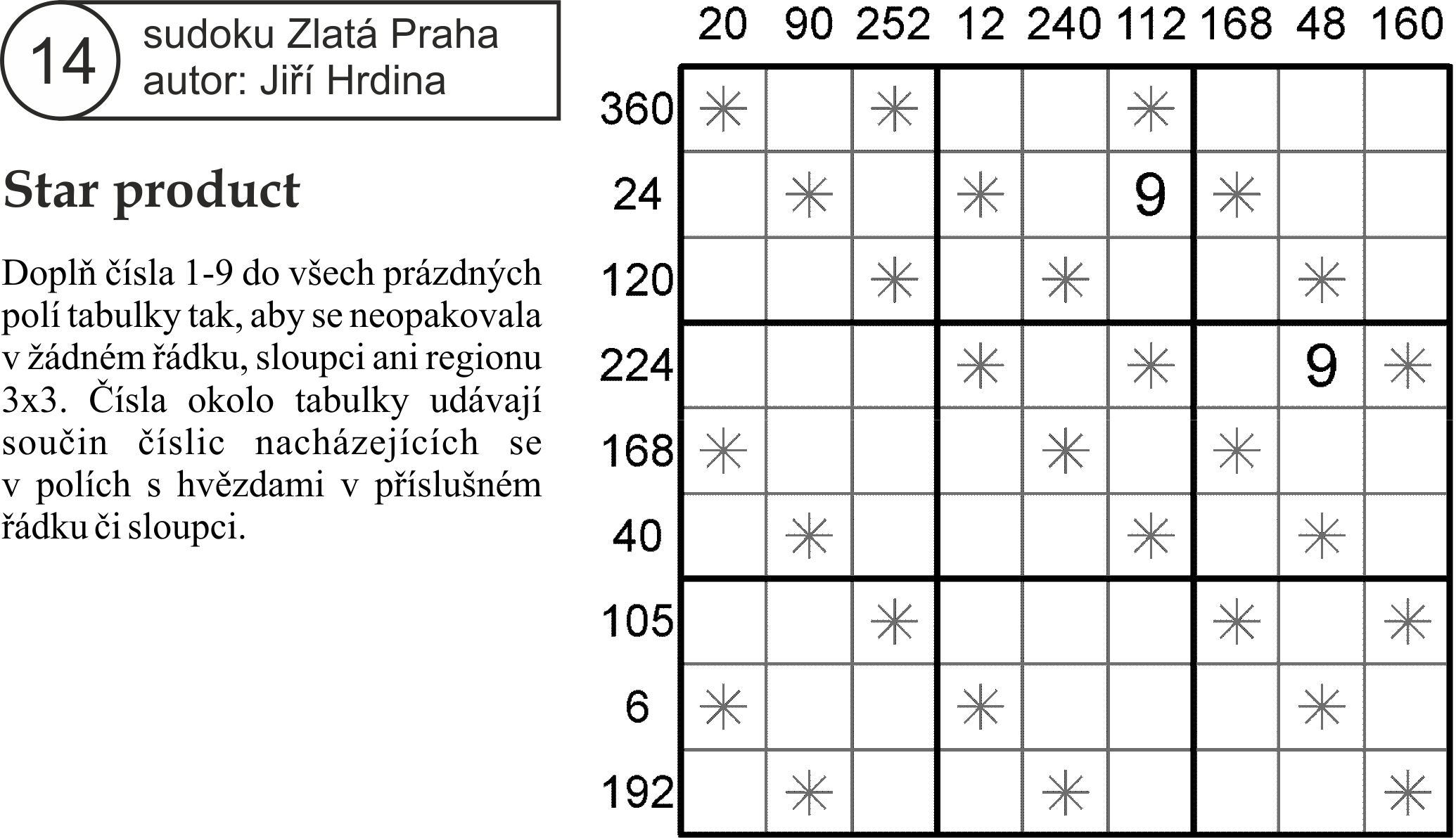
Úvodem si zopakujem matematiku ze základky. Čísla, kterými se násobí, jsou činitelé, výsledek je součin. Jestli jste to někdo nevěděl tak si z toho nic nedělejte, já jsem se taky musel podívat na wikipedii :)
Součiny, které končí číslicí 0 nebo 5, musí obsahovat pětku. Navíc platí, že součiny, které končí jinou číslicí než 0 a 5, pětku obsahovat nemohou. Začneme tedy tím, že vyhledáme součiny dělitelné pěti, a pokusíme se pětky dosadit.
Podíváme-li se např. na první řádek, 360 je dělitelné pěti, na jedné ze tří hvězd v tomto řádku tedy musí být pětka. Tyto hvězdy se křižují se součiny 20, 252 a 112. Pouze součin 20 může obsahovat pětku, pětka tedy musí být na pozici ř1s1. Stejným principem dosadíme do tabulky další tři pětky.
Můžeme také využít toho, že pokud je součin lichý, všechny činitelé musí být liché. U této úlohy se to týká pouze součinu 105, který bude obsahovat 357. Jednička se do tak vysokého součinu nevejde, devítkou není číslo 105 dělitelné (105-90=15). Nakonec to ale není potřeba, pětku lze dosadit snadno na místo křížení se součinem 160, pak už ty zbylá čísla jde snadno dopočítat (21 může být pouze 37).

Dále můžeme využít toho, že součiny, které nejsou dělitelné pěti, pětku obsahovat nemůžou. Podíváme-li se na 2. řádek, pětka může být pouze na dvou políčkách. Jedno z nich obsahuje hvězdu, která náleží součinům 24 a 168. Pětku můžeme z tohoto políčka vyloučit a dosadit do pozice ř2s8.
To samé lze udělat ve 4. řádku. Pětka nemůže být na žádné z hvězd, neboť tyto hvězdy náleží součinu 224. Pětku proto dosadíme na pozici ř4s7.

Dále se podíváme na součiny, do kterých jsme si dosadili pětku, a ovpiskujeme si zbylé hvězdy. Pro větší přehlednost jsem políčka s hvězdou vybarvil.
V prvním sloupci mohou být na zbylých hvězdách pouze čísla 1 a 4 (20:5=4), jediná kombinace pro součin 6 v 8. řádku je 123, jediný společný vpisek je 1, pole ř8s1 tedy obsahuje jedničku.
Do prvního řádku doplníme vpisky 89 (360:5=72, jediná kombinace pro 72 je 8x9).
Jediná kombinace pro 5. řádek je 67 (168:4=42).
V sedmém řádku vzniknou vpisky 37 (105:5=21).
Do posledního sloupce můžeme doplnit vpisky 48 (160:5=32, jediná kombinace pro 32 je 4x8).
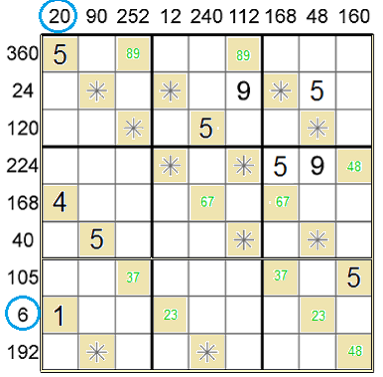
5. sloupec může obsahovat pouze 68 (240:5=48, jediná kombinace pro 48 je 6x8), na místě křížení se součinem 168 může být pouze šestka, doplnit můžeme i osmičku na pozici ř9s5 a sedmičku na pozici ř5s7. Tato sedmička rozhodne dvojici 37 v sedmém řádku.
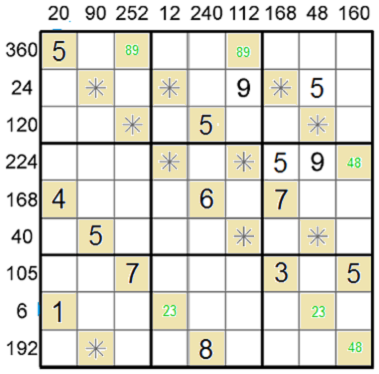
Čerstvě doplněná trojka rozhodne dvojici 23 v 8. řádku.
Přehlídnul jsem, že dvojice 89 v 1. řádku šla rozhodnout z fleku podle zadané devítky ve 2. čtverci, takže to tam doplním teď.
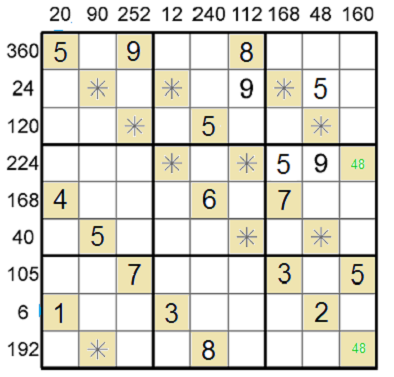
Osmička v 9. řádku rozhodne dvojici 48 v 9. sloupci.
Následně můžeme v 9. řádku dopočítat součin 192. (192:8=24, 24:4=6). Na pozici ř9s2 tedy doplníme šestku.
Dopočítáme i součin ve 2. sloupci (90:5=18, 18:6=3).

Dopočítáme součin 112 v 6. sloupci (112:8=14). Jediná kombinace pro 14 je 2*7, jelikož 40 není dělitelné sedmi, doplníme sedmičku do prostřední hvězdy a dvojku do spodní.
Nově doplněná dvojka pomůže dopočítat součin 40 (40:5=8, 8:2=4). Do políčka ř6s8 doplníme čtyřku.

Teď koukám že jsem složitě dopočítával součin 112, přitom ve 4. sloupci šlo mnohem jednodušeji dopočítat 12 jako 1*4, přičemž jednička nemůže být v součinu 3 čísel s výsledkem 224.
Poté snadno dopočítáme 2. řádek (24:3=8, 8:1=8) a 8. sloupec (48:2=24, 24:4=6).
Čerstvě doplněná šestka pomůže dopočítat 3. řádek (120:5=24, 24:6=4).
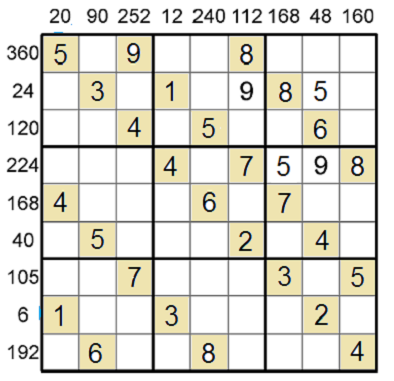
Teď už máme všechny hvězdy vyplněné, zbývá nám tedy už jen dohrát tabulku jako klasické sudoku.

Postup sepsal Honza Zvěřina.
Theme by Danetsoft and Danang Probo Sayekti inspired by Maksimer