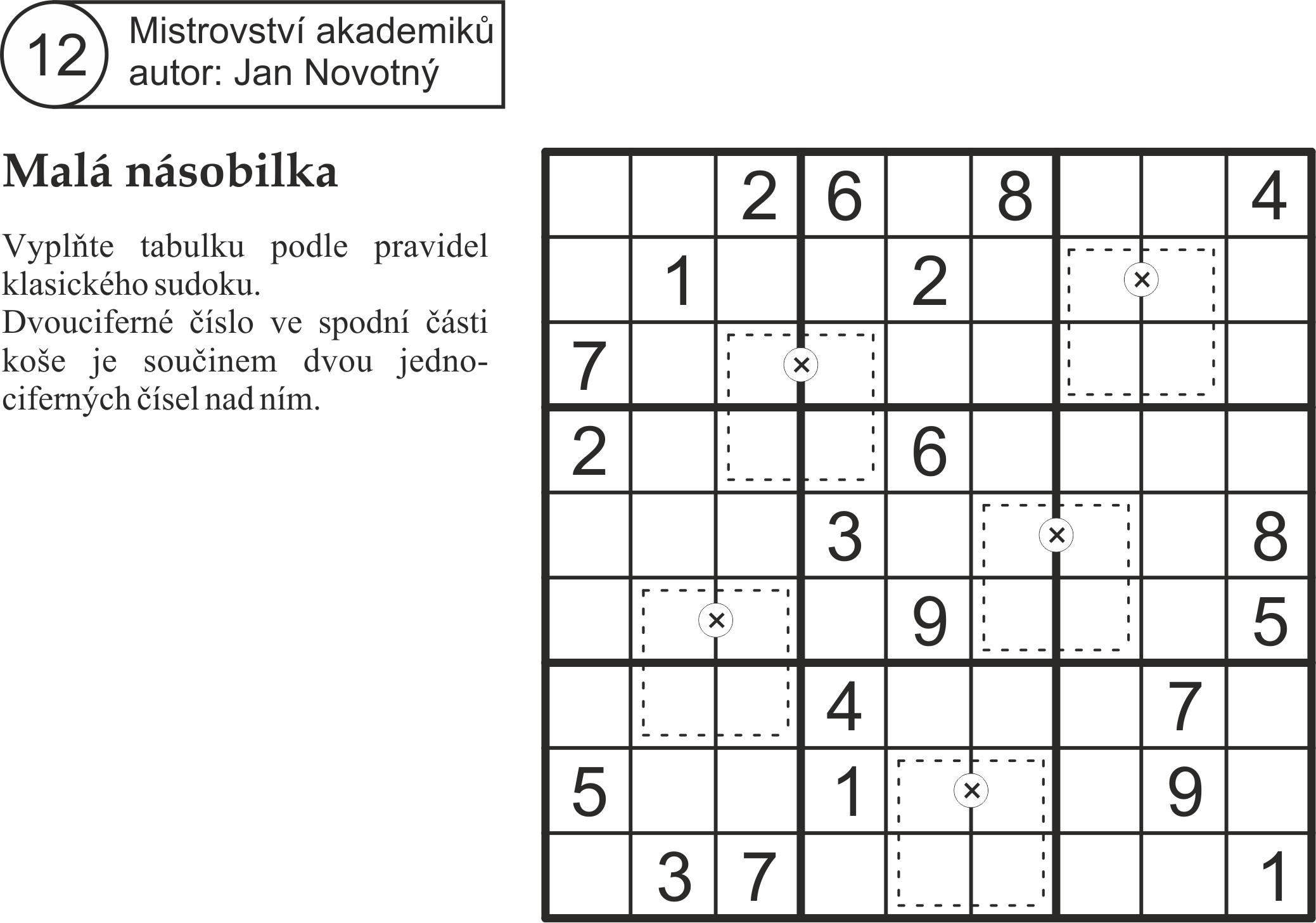
Na začátek je třeba si uvědomit zvláštní postavení čísla 5 v této úloze: Ve čtverečkách s násobením se pětka nikdy nemůže vyskytovat na prvním řádku vpravo, protože výsledkem násobení pěti by byla nula nebo pětka na místě jednotek v součinu, která je s ní ve stejném sloupci. Jako levý činitel přichází pětka v úvahu pouze tehdy, zasahuje-li čtvereček s násobením do dvou různých čtverců mřížky. Je-li pětka jedním z činitelů, musí na místě druhého činitele stát liché číslo.
Pole 95 (řádek 9, sloupec 5): může obsahovat jen čísla 5 nebo 8. Osmička nepřichází v úvahu, protože žádný součin dvou různých jednociferných čísel nezačíná 8 --> 955, 775, 185
1. řádek: je třeba doplnit 1,3,7,9: 129, 113
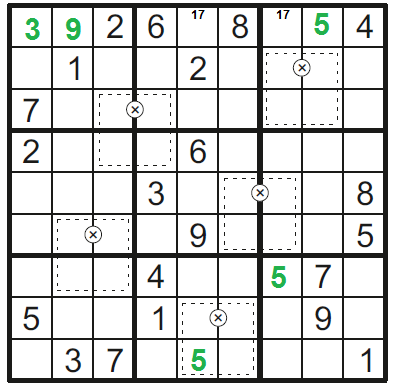
Na 34 může být jen 9 (5 ne, viz výše)
33: nabízí se 4,5,6,8, z toho se hodí jen 5 (ostatní čísla by dala s devítkou součin, který do mřížky nelze zapsat --> 335, 434, 445, 285, 525
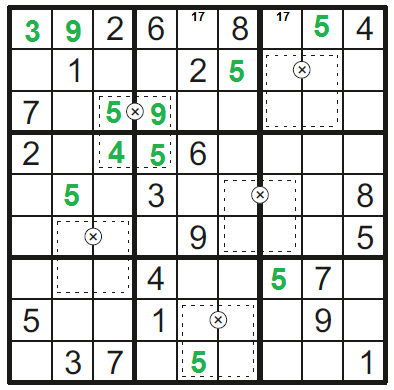
Součin na 9. řádku začíná pětkou, může to tedy být jen 54 (9x6) nebo 56 (7x8) --> 858, 867, 966.
Doplníme 8. čtverec – 753, 912, 769, z toho dále 919, 539, 633.
Při pokusu doplnit 3. sloupec vychází 836, z toho pak 796, 824, 722, 238, 731, 718.
V 1. čtverci 326, 214.
2. čtverec: 627 (7x3=21), 428
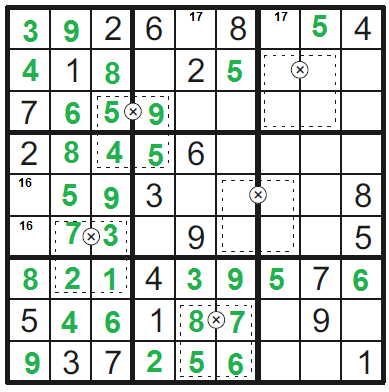
4. sloupec: 247, 648 --> 151, 177, 354, 363, 557
3. řádek: 392, a kvůli součinu (81 není součin dvou různých jednociferných čísel) 371, 388.
2. řádek: z čísel 3,6,9 dá součin 18 3x6 --> 299.
Doplníme 9. sloupec: 893, 497 a 9. čtverec: 872, 984, 978
4. řádek: 461, 483, 479 --> 286, 273
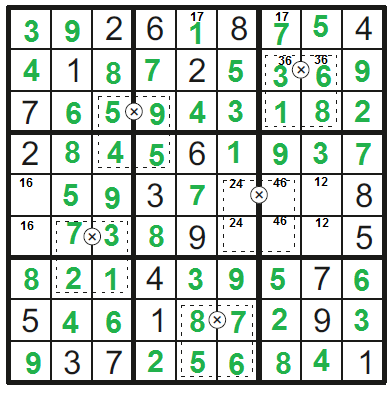
Zbývá vyřešit násobení na řádcích 5 a 6: očividně se jedná o operaci 4x6=24 --> 564, 576, 662, 674.
Doplníme dvojičky v 1. a 8 sloupci a je hotovo ![]()
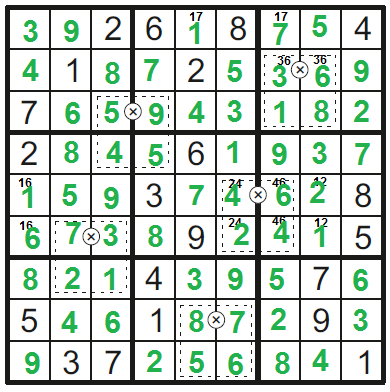
Postup sepsala Jana Zachová.
Theme by Danetsoft and Danang Probo Sayekti inspired by Maksimer