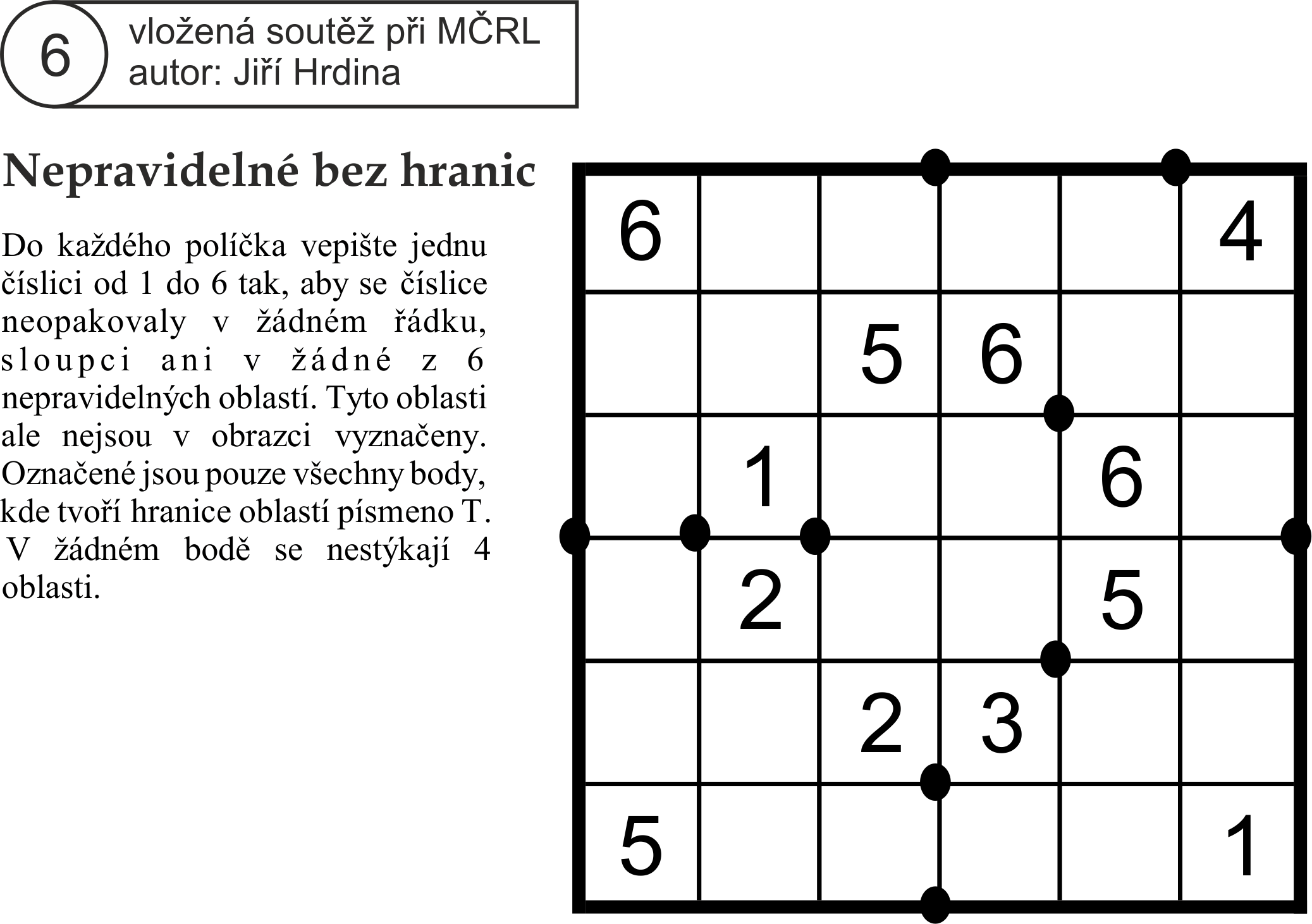
Tam, kde jsou na okrajích mřížky (řádky 1, 6 a sloupce 1,6) vyznačeny tečky, nakreslíme hranice, aby tak vznikl tvar T. Naopak tam, kde na okrajích tečky nejsou, nemůže hranice probíhat (hvězdičky znamenají propojení dvou polí do jedné oblasti).
Při okrajích mřížky tedy vznikají tyto propojené oblasti (souřadnice polí: první číslo udává řádek, druhé sloupec):
A: 31, 21, 11, 12, 13, ?
B: 41, 51, 61, 62, 63, ?
C: 64, 65, 66, 56, 46, ?
D: 16, 26, 36, ?, ?, ?
E: 14, 15, ?, ?, ?, ?
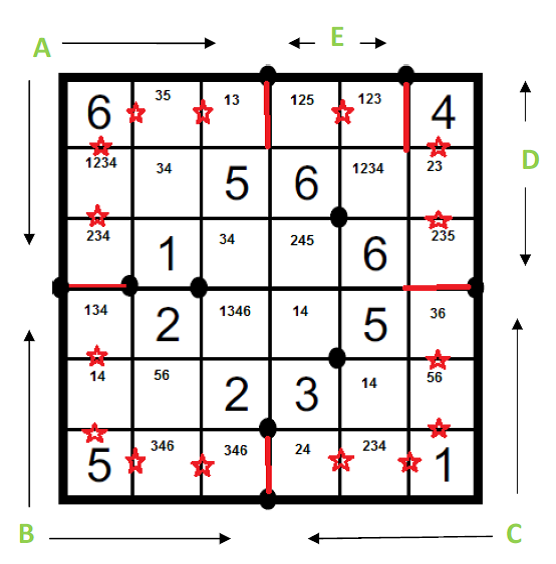
Oblast B: Šesté číslo musí být dvojka, proto můžeme pole 52 od této oblasti oddělit (|51-52, |52-62).
Jednička pro tuto oblast musí být nutně v prvním sloupci, proto můžeme odstranit jedničku z pole 21.
V důsledku toho 251, 554, 511.
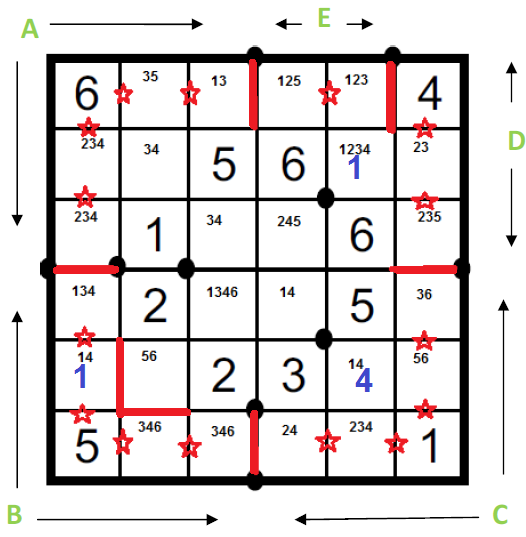
Kdyby procházela mezi poli 35 a 36 hranice, vedlo by to ke splynutí oblastí D a E. Proto mezi 35 a 36 namalujeme hvězdičku. Ze stejného důvodu přijde hvězdička i mezi 14 a 24.
Oblast C: Kdyby šestým číslem této oblasti byla pětka na 45, vypadal by sloupec 6 (čteno shora dolů) takto: 425361 --> oblast D, která je zatím tvořena čísly 4256, nemá nikde v dosahu trojku. Pětku na 45 tedy od oblasti C oddělíme hranicí (zatím jen |45-46).
A přimalujeme hvězdu mezi pole 35 a 45, aby nevzniklo T na místě, kde není vyznačeno.
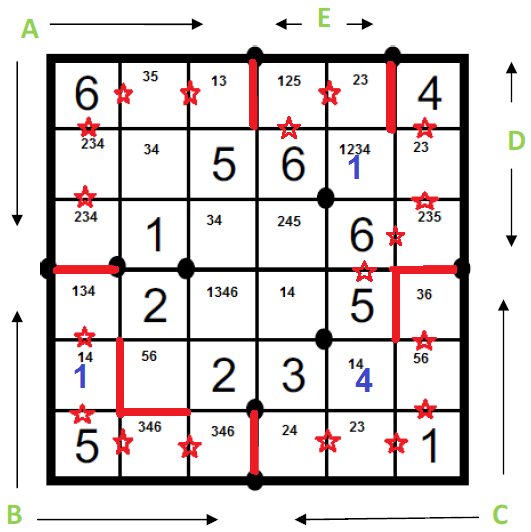
Teď je již jediná pětka pro oblast C k dispozici v poli 56 --> 565, 526, 636, 466, 125, 345
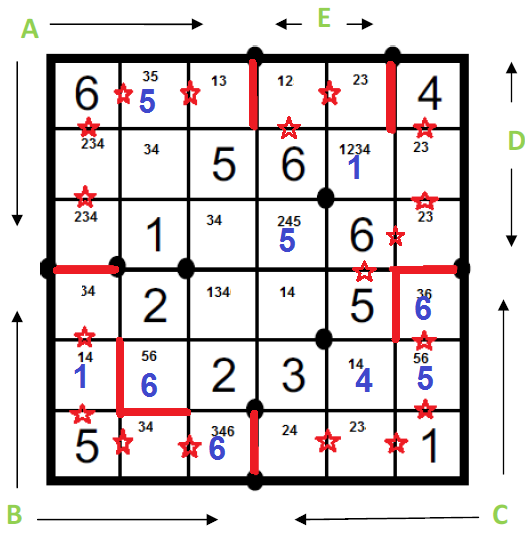
Oblast A: Pětka na 23 nepatří do oblasti A --> oddělit hranicí |13-23.
Zároveň spojit 23 a 26 hvězdou, aby nevzniklo nevyznačené T.
Mezi 45 a 55 musí být hranice, jinak by vznikla propojená oblast (D), obsahující dvě čtyřky.
55 tedy patří do oblasti C, kterou již můžeme vyznačit celou.
Pak 642, 653, 624, 223, 262, 363, 334, 312, 214, 413, 431, 444, 141, 133, 152.
A dokreslíme hranice oblastí:
A: 13, 12, 11, 21, 31, 32
B: 41, 51, 61, 62, 63, 53
D: 16, 25, 26, 35, 36, 45
E: 14, 15, 22, 23, 24, 33
Uprostřed vznikla oblast F: 34, 42, 43, 44, 52, 54.
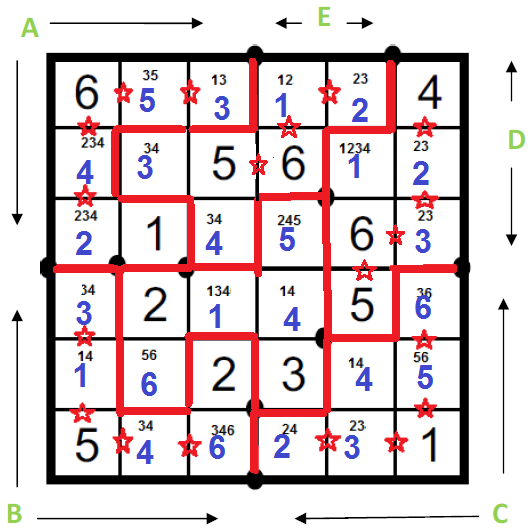

Postup sepsala Jana Zachová.
Theme by Danetsoft and Danang Probo Sayekti inspired by Maksimer