Sousledné sudoku

Pravidla: Platí standardní pravidla sudoku a navíc tlusté čáry označují všechny páry sousedních čísel, která se liší o jedničku.

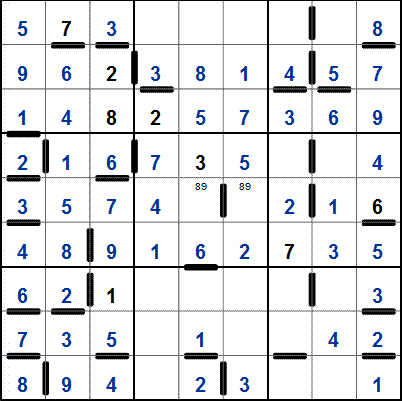
Zadání (06/2012 www.fed-sudoku.eu):

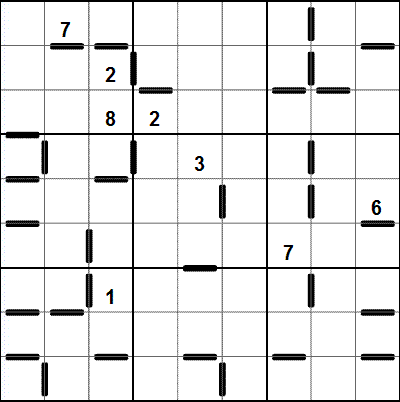
Postup řešení:

R7C2=2
R8C2=3
vyplývá z vyznačených sousledností
R6C9=5
ze souslednosti kandidáti 57, 7 je již ve čtverci
R1C3=3
ze souslednosti kandidáti 13, 1 je již ve sloupci
R2C2=6
ze souslednosti kandidáti 68, 8 je již ve čtverci
v 7. čtverci máme dva sousledné "řetízky", tzn. možnosti rozdělění zbývajících číslic: 4567 a 89, nebo 45 a 6789
v kratším "řetízku" není 8 (je již ve sloupci) => jedná se tedy o variantu 45 a 6789
R9C3=4 (4 nesmí být na pozici R8C3 vedle 3 (na pozici R8C2))
R8C3=5;
na pozici R9C2 (na začátku delšího "řetízku") jsou kandidáti 69, 6 je již ve sloupci, tzn. začneme číslicí 9:
R9C2=9
R9C1=8
R8C1=7
R7C1=6
ve 3. sloupci zbývají kandidáti 679, potřebujeme souslednou dvojici a číslici zvlášť => 67 bude sousledné, 9 je zvlášť
R6C3=9
R5C3=7 (7 nesmí být na pozici R4C3 vedle 8 (na pozici R3C3))
R4C3=6
R6C2=8
vyplývá z vyznačené souslednosti
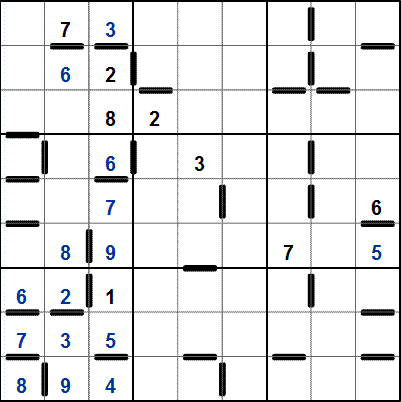
ve 4. čtverci máme sousledný "řetízek" a číslici zvlášť, tzn. možnosti rozdělení zbývajících číslic: 1234 a 5, nebo 1 a 2345
5 nesmí být na R6C1 (je již ve sloupci), ani na R4C2 (nesmí být vedle 6 (na pozici R4C3)) => jedná se tedy o variantu 1234 a 5
R5C2=5
na pozici R4C2 (na začátku "řetízku") jsou kandidáti 14, 4 nesmí být vedle 5 (na pozici R5C2), tzn. začneme číslicí 1:
R4C2=1
R4C1=2
R5C1=3
R6C1=4
R3C2=4
poslední kandidát ve sloupci
R3C1=1
vyplývá z vyznačené souslednosti;
zbývají kandidáti 59, 5 nesmí být na pozici R2C1 vedle 6 (na pozici R2C2):
R2C1=9
R1C1=5
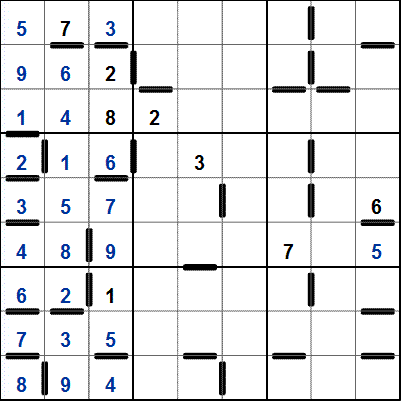
R6C8=3
poslední pozice pro 3 v 6. čtverci
v 6. řádku zbývají kandidáti 126, potřebujeme je rozmístit tak, aby nevznikla žádná souslednost (oddělit číslice 1 a 2 číslicí 6), tj. možnosti jsou 162, nebo 261 (psáno zleva doprava)
na pozici R6C4 jsou tedy kandidáti 12, 2 je již ve sloupci => jedná se o variantu 162:
R6C4=1
R6C5=6
R6C6=2
R2C4=3
ze souslednosti kandidáti 13, 1 je již ve sloupci
v 8. čtverci může být 3 jen na pozicích R7C6, nebo R9C6, na R7C6 není (nesmí být vedle 2 (na pozici R6C6)):
R9C6=3
R9C5=2
ze souslednosti kandidáti 24, 4 je již v řádku
R8C5=1
vyplývá z vyznačené souslednosti
v 9. čtverci může být 3 jen na pozicích R7C7, nebo R7C9; bude-li na R7C7, pak na R7C8 budou kandidáti 24 (vyplývá ze souslednosti), což je spor (oba tito kandidáti by byli souslední s 3 (na pozici R6C8), avšak tam není souslednost vyznačena):
R7C9=3;
od 3 (na pozici R7C9) je možné rozvinout sousledný "řetízek" 321 nebo 345 (psáno shora dolů), 5 již ve sloupci je => jedná se o variantu 321:
R8C9=2
R9C9=1
R3C7=3
poslední pozice pro 3 ve 3. čtverci
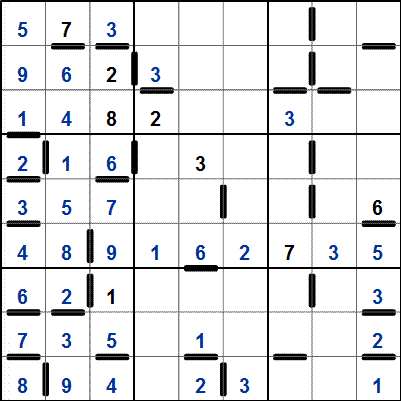
od 3 (na pozici R3C7) je možné rozvinout sousledný "řetízek" 3456:
R2C7=4
R2C8=5
R3C8=6
v 9. čtverci může být 4 jen na pozicích R7C8, nebo R8C8, na R7C8 není (nesmí být vedle 3 (na pozici R7C9)):
R8C8=4
v 6. čtverci může být 2 jen na pozicích R5C6, nebo R5C8, na R5C8 není (nesmí být vedle 3 (na pozici R6C8)):
R5C7=2
R5C8=1
vyplývá ze souslednosti
R4C9=4
poslední pozice pro 4 v 6. čtverci
v 5. řádku zbývají kandidáti 489, potřebujeme souslednou dvojici a číslici zvlášť => 89 bude sousledné, 4 je zvlášť
R5C4=4
na pozicích R4C4 a R4C6 zbývají kandidáti 57, 5 nesmí být na pozici R4C4 vedle 4 (na pozici R5C4):
R4C4=7
R4C6=5
R3C5=5
poslední pozice pro 5 ve 2. čtverci
ve 3. řádku zbývají kandidáti 79, 7 nesmí být na pozici R3C9 vedle 6 (na pozici R3C8):
R3C6=7
R3C9=9
v 9. sloupci zbývají kandidáti 78, 8 nesmí být na pozici R2C9 vedle 9 (na pozici R3C9):
R1C9=8
R2C9=7
ve 2. řádku zbývají kandidáti 18, 8 nesmí být na pozici R2C6 vedle 7 (na pozici R3C6):
R2C5=8
R2C6=1
v 5. čtverci zbývají kandidáti 89, 8 je již v 5. sloupci:
R5C5=9
R5C6=8
v 8. čtverci může být 5 jen na pozicích R7C4, nebo R9C4, na R9C4 není (nesmí být vedle 4 (na pozici R9C3)):
R7C4=5
R7C5=7
poslední pozice pro 7 v 8. čtverci
R7C6=4
poslední pozice pro 4 v 8. čtverci
R8C4=8
poslední pozice pro 8 v 8. čtverci
R8C6=9
poslední pozice pro 9 v 8. čtverci
R9C4=6
poslední kandidát ve čtverci
R1C4=9
R1C5=4
R1C6=6
umísťováno pomocí pravidel klasického sudoku
R9C7=5
R8C7=6
R9C8=7
umísťováno pomocí pravidel klasického sudoku
v 9. čtverci zbývají kandidáti 89, 8 nesmí být na pozici R7C7 vedle 7 (na pozici R6C7):
R7C7=9
R7C8=8
R4C7=8
R4C8=9
umísťováno pomocí pravidel klasického sudoku
R1C7=1
R1C8=2
umísťováno pomocí pravidel klasického sudoku
hotovo :o)